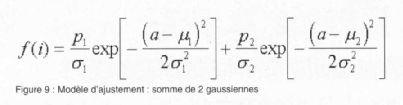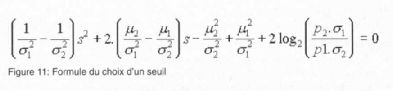Suivez-nous sur X

|
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z,
ALL
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
A propos d'Obligement

|
|
David Brunet

|
|
|
|
Dossier : Le traitement d'images numériques - Quadtree et découpages itératifs
(Article écrit par Barrou Diallo et extrait d'Amiga News - janvier 1997)
|
|
Après les petites transformations géométriques du mois dernier, nous allons revenir à
des propos un peu plus orientés "traitement du signal" et étudier encore quelques méthodes pour torturer ces fameuses images.
Suite à de nombreuses remarques de lecteurs qui voulaient obtenir des documentations sur les différentes applications qu'ils
font du traitement d'images, je vais essayer de rester assez généraliste dans le sens de mon exposé. Cette matière a la chance
d'être utilisée dans des milieux aussi différents que l'industrie lourde, la détection d'objets volants à l'armée, la
quantification de tumeurs dans le monde biomédical, la reconnaissance de caractères manuscrits, l'analyse de scène en
visionique, l'hydrométrie dans l'imagerie satellite et tant d'autres domaines que j'oublie. Cette variété d'application
entraîne automatiquement une variété d'approches dans les problématiques. Images à canal unique versus multicanaux, images
paramétriques ou symboliques, images bruitées ou floues. Bref, les problèmes dans la reconnaissance de forme et l'interprétation
automatique de scène ne manquent pas.
Le partitionnement des images
Une approche assez classique en logique est de résoudre un problème en essayant de le sous-diviser en plusieurs parties qui
sont autant de nouveaux petits problèmes plus faciles à résoudre. Merci à M. Descartes qui a jeté les bases de ce principe
que l'on applique aujourd'hui (entre autres) à l'image. Mais comment décomposer une image ? Il existe évidemment plusieurs
méthodes : la décomposition spectrale (Transformée de Fourrier) ou des transformations plus "algorithmiques" basées sur la
géométrie discrète.
Le quadtree
La première idée qui vient à l'esprit lorsque l'on veut découper une image est de la diviser en deux, puis en quatre, puis
en huit et ainsi de suite. Ce découpage par pavages carrés réguliers est appelé quadtree. Ce terme désigne un arbre (au sens
structure de données du terme) composé de zones carrées qui composent ses feuilles. Nous avons ici une représentation typiquement
récursive : soit une image que l'on découpe en quatre et pour chacun des morceaux on réapplique ce découpage. Ce processus peut
être itéré jusqu'à la notion de pixel (qui prend ici tout son sens). Si l'image fait une taille NxN, alors le nombre de
découpage (le nombre de niveaux dans l'arbre) est de N+1. La figure 1 présente une image binaire en noir et blanc très simple qui
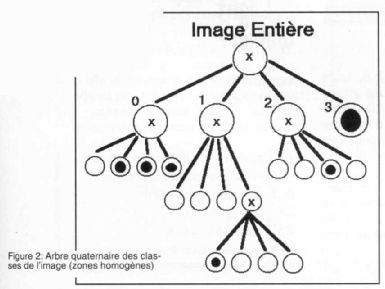
a été découpée selon le principe expliqué ci-dessus. De ce découpage, résulte l'arbre de la figure 2 qui comporte trois type
de noeuds : les noeuds x qui représentent les zones non homogènes, les noeuds noirs et les noeuds blancs. Chaque noeud peut
être numéroté comme le montre la figure 3. Cette numérotation est importante et attribue en quelque sorte un "label" à une zone,
ce qui permettra plus tard de passer de coordonnées 2D à des valeurs uniques.
L'application de ce découpage peut se faire sur une image binaire ou en niveaux de gris. Chaque bloc représente alors une zone
dite "homogène". Le critère d'arrêt du découpage est simple sur une image binaire : si la zone contient à la fois des pixels
noirs et des pixels blancs, alors, il faut la redécouper de nouveau. Sinon, il faut s'arrêter et considérer que la zone est
homogène.
Dans une image en niveaux de gris et, pire encore, sur une image couleur, les critères d'arrêts sont loin d'être évidents.
Différentes approches ont été mises en œuvre et nous pouvons citer, entre autres, l'analyse des textures de la scène, les
calculs de variances et de moyennes, les approches de la théorie de l'information ainsi que d'autres critères plus "physiques"
comme le critère d'hystérésis. La construction d'un quadtree est donc liée à une recherche d'homogénéité (variance minimale,
attributs semblables, etc.). Une fois cet arbre construit, seule la première étape est achevée. La seconde consiste à rassembler
les zones suivant d'autres critères moins abrupts que le découpage par pavages. On appelle cette étape la fusion de zone. Là
encore, de nombreuses méthodes permettent de fusionner ou regrouper des zones arbitrairement séparées. Nous y reviendrons
plus tard.
Prenons d'abord le temps d'expliquer l'implémentation de ce type d'arbre qui, il est vrai, soulève des questions intéressantes
du point de vue programmation. Le découpage récursif consomme à la fois du temps de calcul et de la mémoire. Même si, de nos
jours, ces deux paramètres sont de moins en moins importants, une mauvaise implémentation du quadtree entraîne une perte de
temps considérable.
Vision simpliste du découpage récursif :
Procédure DécoupeZone (StructZone zone)
Début
Si zone != Homogène Alors
DécoupeZone (zone)
Sinon
Stocke les paramètres
Fin
Cette façon de coder une arborescence est intuitive mais, reste inadaptée aux ordinateurs de bureau. Cette fonction récursive
(qui se rappelle elle-même) construit via la pile système l'arbre quaternaire de l'image. Mais, comme la pile n'est pas infinie,
cette méthode est très dépendante de la taille de l'image. En fait, la représentation mémoire de l'arbre nécessite la mise en
oeuvre de pointeurs (ou d'adresses de cases), ce qui alourdit le processus. L'arbre est construit à partir de la racine et donc
tous les pixels sont consultés un nombre de fois équivalent au nombre de niveaux dans lequel il apparaît. Le test d'homogénéité
d'une zone est effectué pour tous les pixels d'une zone. Cette zone pouvant être découpée, il sera de nouveau effectué sur ces
pixels. Bref, le coût en temps de calcul n'est plus à démontrer, il faut donc trouver une astuce d'implémentation.
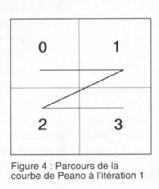
L'une des implémentations les plus astucieuses est celle utilisant le codage de la courbe de Peano en Z. A la première itération,
les zones sont parcourues dans un sens strict (celui de Peano) comme le montre la figure 4. Ce parcours est répété pour toutes
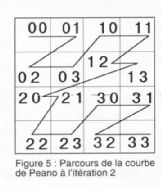
les récursions de toutes les zones. La figure 5 montre la courbe de Peano à l'itération 2. Il faut ainsi de suite redécouper les
zones et agrandir cette fameuse courbe. Les propriétés de cette courbe sont immenses et vous remarquerez que si l'on pousse le
processus jusqu'à son terme, c'est-à-dire le pixel, on remplit le plan grâce à une courbe en une dimension ! Elle permet donc de
passer d'une dimension à une autre, et là, la théorie des fractales prend tout son sens.
A une itération i, quelle est la dimension fractale de la courbe de Peano ? Ni 1 ni 2, elle a une dimension non entière, elle est
donc fractale. Nous pourrons revenir aux applications des fractales dans le domaine du traitement de l'image lors d'autres
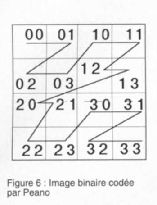
articles mais, notez seulement que ce codage permet de coder une position par un nombre en base 4. La figure 6 montre une image
(boules noires) codée par cette méthode. On détecte trois objets {02} {13} et {3}. Le fait de coder une image de la sorte entraîne
un gain de place et de parcours. Toute l'information de cette image binaire peut donc être comprimée en ces trois
nombres grâce à la courbe de Peano. Le nombre de chiffres qui le composent donne automatiquement le niveau d'itération et par une
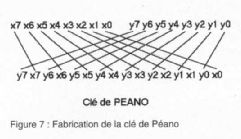
astuce de codage, il est possible d'associer à chaque pixel (x,y) un nombre sur la courbe de Peano. Cette méthode, qui est une
bijection de N2 dans N, est appelée clé de Peano. Elle est formée en intercalant les bits des coordonnées pixels (x,y) un à un.
La figure 7 montre cet intercalage qui forme la clé pour passer d'un espace à l'autre. A un couple de coordonnées correspond donc
une valeur unique donnée par la clé.
Remarques et restrictions
Cette méthode ne peut s'appliquer que sur des images carrées ou centrées dans une grande image carrée. La largeur ou longueur
des carrés est une puissance de deux ce qui a permis l'analogie avec le codage binaire. Bref, cette structure est bien adaptée
à l'esprit d'un ordinateur et donc d'un informaticien. Ensuite, on remarquera que ce découpage arbitraire en carrés égaux est
grossier et inadapté à des images naturelles. Notons tout de même un avantage : cette méthode n'est pas dépendante de la
dimension de l'image, on peut l'appliquer à des images 3D, à des séries de coupes conjointes ou même à des séries temporelles
dans le but d'une compression d'informations.
Une approche commune
Il existe toutefois un invariant dans cette diversité d'algorithmes : le traiteur d'images en revient souvent à cette notion
d'histogramme et de seuillage. Tout commence ou se termine par un seuillage dira-t-on ? Presque, car un seuillage qu'il soit
simple ou multiple équivaut, dans la pratique, à créer des zones de pixels isoprobables. Voyons maintenant la méthode proposée
par Nakagawa qui consiste comme nous l'avons montré plus haut à découper l'image en zones d'intersection vide dans lesquelles
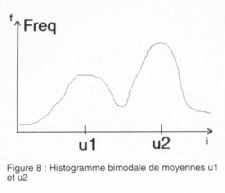
on calcule l'histogramme. Cet histogramme est approximé par deux gaussiennes si l'écart entre les deux modes (Cf. figure 8)
est suffisant. Il ne faut pas oublier de lisser cet histogramme en appliquant soit un filtre moyenneur, soit un filtre médian
1D sur trois valeurs consécutives. La figure 9 représente la formule qui permet d'approximer un histogramme bimodal par la
somme de deux lois de Gauss. Il y a donc six paramètres à ajuster pour approcher ce modèle. Le critère utilisé par Nakagawa
est simple à calculer. Une zone est considérée comme bimodale si et seulement si :
- 1. u2-u1 > 4
- 2. 0.1 < sigma1 / sigma2 < 10
- 3. delta < 0.8
u1 et u2 sont les moyennes des modes de l'histogramme. Sigma1 et sigma2 sont les écarts-types de l'histogramme, delta est le
résultat de la formule donnée en figure 10.
Si l'histogramme de la zone en cours est considéré comme bimodal, alors, on applique la formule 11 qui consiste à minimiser
l'erreur d'une mauvaise séparation des pixels sachant la distribution observée (f). La valeur "s" est le seuil à appliquer.
Ce seuillage donne de bons résultats si les distributions sont à peu près gaussiennes. Il est appelé dynamique et adaptatif
car le découpage successif de l'image permet de s'affranchir des hétérogénéités de spatiales.
Conclusion
Nous avons étudié deux grandes méthodes de segmentation qui sont le quadtree et le découpage adaptatif en vue d'un seuillage.
Ces méthodes, loin d'être neuves, sont très utilisées de par leur simplicité de programmation, et la qualité des résultats.
Elles reposent le problème de la qualité versus la rapidité. Il est encore difficile d'avoir ces deux paramètres complètement
décorrélés. Il n'est, par exemple, pas possible d'effectuer ces traitements en temps réel sur une chaîne de montage dans
l'industrie... Après cet exposé un peu plus approfondi, nous reviendrons à d'autres méthodes de partitionnement tout aussi
efficaces, mais peut-être encore une fois assez lentes à mettre en oeuvre.
Références :
Samet H : The Quadtree and related hierarchical data structures, Computing Surveys, vol 18n p298-303, 1982.
Nakagawa Y., Rosenfeld, A. : Some experiments on variable thresholding, Pattern Recognition, vol 11, p191-204, 1979.
Meagher, D. : Geometric Modeling using octree encoding, Computer graphics and image processing, vol 19., p129-147, 1982.
|