 |
Mardi 23 décembre 2025 - 11:03 |
| Translate |
|
| Rubriques |
| Réseaux sociaux |
|
| Liste des jeux Amiga |
|
| Trucs et astuces |
|
| Glossaire |
|
| Galeries |
|
| Téléchargement |
|
| Liens |
|
| Partenaires |
|
| A Propos |
|
| Contact |
|

|
|
MandelTour est un programme convivial et puissant, destiné à permettre la découverte et l'exploration des fractales de Mandelbrot et de Julia, avec en prime une ouverture sur une variété de ces fractales fort peu connue à ce jour. Mais chut... ça, c'est la surprise.
Je vous ai déjà dit dans un entrefilet d'un article précédent tout le bien que je pense de MandelTour. J'ai plaisir à vous le présenter un peu plus en détail aujourd'hui, même si les premières lignes de l'article racontent une petite mésaventure.
Installation
Un très bref coup d'oeil au texte d'introduction montre que l'installation sur disque dur est ultra-simple, allons-y de bon coeur. On recopie les fichiers de la disquette dans un tiroir ad hoc, on clique sur les icônes et hop, un joli Mandelbrot apparaît, avec au centre, le texte "Bienvenue dans l'ensemble de Mandelbrot !". Nous avons affaire à un auteur courtois.
Bon, un clic droit de la souris, et... pas de menu en vue. Mais il y a dans le haut de l'écran une vague lueur blanche qui exprime comme un appel muet et pathétique. J'avance la souris sur le tapis, puis sur la table, mon bras droit en complète élongation et le nez dans l'écran (flûte, il va falloir renettoyer le filtre), et voilà que descend du plafond un morceau de menu. Ah... s'il y en a un, il y en a d'autres. Je déplace mon bras à droite, lequel pousse la tasse de thé que ma charmante épouse vient de m'apporter. Heureusement, ladite tasse rencontre après 5 mm de glissade l'imprimante qui se trouvait là, le mouvement n'a pas suffi à créer une vague telle que le liquide brûlant et surtout sucré se répande parmi les trucs divers que l'on trouve sur tout bureau d'amigoïde. Quelle aventure !
C'est alors que me revient, telle une image fulgurante, un mot que mon inconscient a enregistré au milieu d'une icône : "overscan" (suraffichage). Eh oui, MandelTour s'ouvre en suraffichage, et même en suraffichage sévère, soit 368x283, soit le maximum alloué par Intuition sous 1.3. Je fais revenir l'écran du Workbench à l'avant-plan, il est tout décalé en haut et à gauche. Aïe aïe aïe ! Le moniteur Commodore A1950, pourtant prévu pour Amiga puisque c'est lui qui doit équiper normalement l'A3000, ne permet pas l'affichage d'un suraffichage de cette largeur. Il n'y a pas de réglage par potentiomètre de l'amplitude horizontale, mais seulement un interrupteur à deux positions, la position "étroite" laissant une bande noire de chaque côté de l'image.
Sur mon vieux 1081, il y a des boutons de réglage des amplitudes horizontale et verticale sur la face arrière, j'espère qu'il en est de même sur les 1083 et 1084. Mais comme nous le verrons plus loin, MandelTour permet parfaitement de s'accommoder de toutes les situations, et passée la surprise du début, on se rend compte de ce que le suraffichage est un de ses points forts.
Documentation
L'auteur de MandelTour, Charles Vassallo, est aussi l'auteur de LirePic, un lecteur de documentation. Inutile de dire que pour expliquer la technique de coloriage d'une image fractale, essentielle pour obtenir des résultats intéressants, le fait de disposer d'une documentation en couleurs est un atout considérable.
Charles Vassallo a pris le parti de créer un programme permettant l'obtention rapide de belles images par tout utilisateur même complètement illettré en mathématiques. C'est dire que la documentation comporte un strict minimum d'information mathématique, dont au demeurant l'illettré mentionné ci-dessus pourra parfaitement se passer. Ceci ne veut pas dire que quelqu'un qui connaît déjà bien les fractales ne pourra pas trouver un intérêt certain dans ce programme. J'y reviendrai.
Utilisation
Tout le plaisir d'une première rencontre avec la fractale de Mandelbrot réside dans l'exploration de l'image, par des zooms de plus en plus profonds, qui révèlent une infinie variété de motifs. On commence par zoomer n'importe où, puis, au hasard des découvertes, on affûte son pifomètre et on commence à trouver des choses vraiment intéressantes.
MandelTour est conçu vraiment pour cela et dans cette optique, c'est une réussite. Je ne vais pas vous décrire les menus par le menu, ni même toutes les fonctions, mais plutôt mettre l'accent sur les originalités de ce programme.
On part de l'image classique du Mandelbrot "pur". En activant la fonction "Zoom avant", on voit apparaître une série de cadres rectangulaires gris. En encadrant approximativement un de ces cadres via un clic maintenu, on accède instantanément à un agrandissement correspondant au contenu de ce cadre. En effet, toute une série d'images précalculées sont fournies sur la disquette, chacune étant associée aux coordonnées d'un des cadres. Il y a donc une partie du travail d'exploration qui est déjà faite, et vous imaginez bien que Charles Vassallo n'a pas choisi ces zones au hasard.
A partir de n'importe quelle de ces images précalculées, on peut, par une fonction "Nouvelle image", faire un zoom sur une partie de l'écran, demander le calcul d'une nouvelle image, puis la jeter, ou demander qu'elle soit incorporée à la bibliothèque d'images précalculées. Vous pourrez donc mener votre exploration sans perdre de temps à recalculer des images intermédiaires, et sans à vous occuper de la gestion des fichiers, le programme le fait pour vous. A la limite, l'utilisateur n'a même pas besoin de savoir ce que c'est qu'un fichier ! Il suffit de savoir manipuler une souris.
Un menu comporte une fonction "Show" qui permet d'afficher en séquence toutes les images de votre bibliothèque, et deux fonctions "Enlève Image" pour alléger la bibliothèque lorsque le disque dur se remplit (ça peut aller très vite ; Charles vous conseille de réfléchir avant de sauver une image. Au début on a tendance à tout garder) et "Ajoute Image" pour ajouter une image venant par exemple d'une autre bibliothèque. Bien sûr, en l'absence certes regrettable mais fort compréhensible d'un disque dur, la gestion de la bibliothèque est possible sur disquettes.
Un des intérêts de ce système est la possibilité d'échanger des bibliothèques entre plusieurs utilisateurs, à condition bien évidemment d'avoir choisi le même format d'écran. On peut bien sûr faire des images en mode haute résolution entrelacé (avec dans ce cas 16 couleurs), mais elles seront sauvées séparément et ne feront pas partie de la bibliothèque.
Fractales de Julia
De manière à suivre la logique de l'auteur, pas d'explication ici de ce qu'est une fractale de Julia. Tout ce qu'il faut savoir pour le moment, c'est que ces images ont la propriété de changer complètement d'aspect en fonction d'un paramètre qui est la position d'un point dans la figure de Mandelbrot ; on appelle ce point le point source.
En mode Julia, on clique sur un point de l'écran puis en répondant à quelques questions simples dans une fenêtre de requête, on obtient une image que l'on peut également stocker dans la bibliothèque. Sur l'image principale de la Mandelbrot, ou sur les images du catalogue, apparaissent des croix grises aux endroits où une image Julia a été calculée, puis sauvée et incorporée dans la bibliothèque.
La figure 1 donne un zoom sur un endroit de la fractale de Mandelbrot, la figure 2 montre une fractale de Julia obtenue en cliquant dans cette zone. Et voilà : ce n'est pas plus difficile que ça !

Figure 1

Figure 2
Mais je vous avais promis une surprise, elle est de taille. Il y a dans le deuxième menu une fonction "Mandelbrot Incomplet", avec cinq options possibles.
Les Mandelbrot incomplets se choisissent comme pour les Julia, en définissant par un clic de souris un point source dans l'image d'un Mandelbrot normal. Seulement, les images obtenues sont assez déroutantes. En mode 1, on y aperçoit, selon la localisation du point source, une sorte de Mandelbrot normal, auquel il manque des morceaux, d'où leur nom (figure 3).
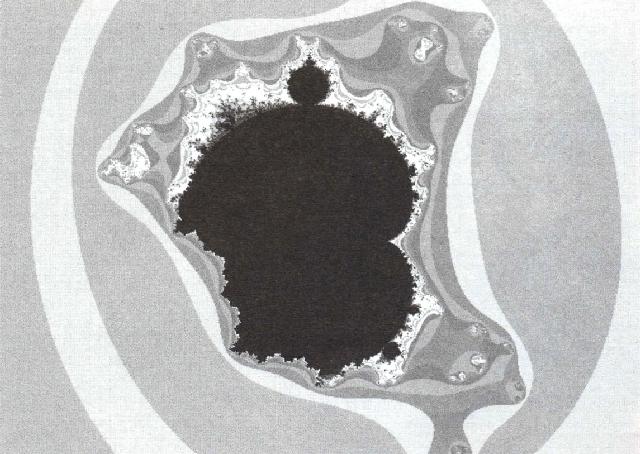
Figure 3
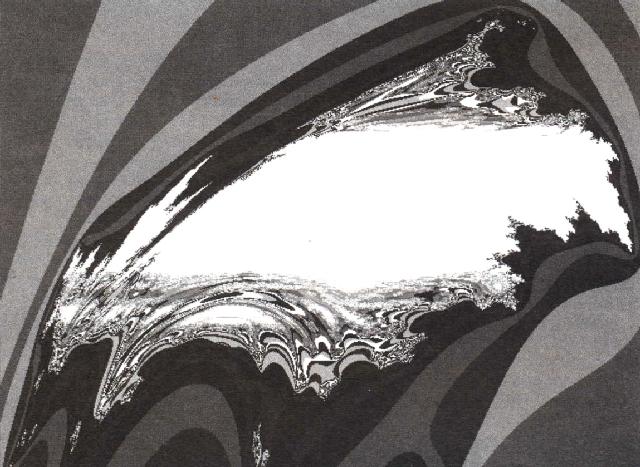
Figure 4
MandelTour calcule ses images de base très vite. Néanmoins, il vient un moment où il faut augmenter le nombre d'itérations, le nombre de chiffres significatifs ou la résolution de l'écran pour obtenir suffisamment de détails et là, ça devient plus long. Sur une machine non accélérée, il y a des images qui prennent plusieurs heures à sortir. C'est là qu'on apprécie les capacités de l'Amiga en multitâche. Pendant que vous faites votre courrier, ou toute autre chose qui ne risque pas de planter la machine ou d'imposer un redémarrage en fin d'exercice (la plupart des jeux, malheureusement), MandelTour ronronne gentiment en arrière-plan. Ça marche d'autant mieux qu'il est lancé avec une priorité comme -5 par exemple. MandelTour peut calculer sur 32, 48 ou 64 bits, ce dernier chiffre correspondant à 15 décimales, ce qui permet des zooms profonds.
Attendez, il y en a encore...
Animations
MandelTour vous permettra sans aucune difficulté de créer des animations. On peut créer une animation, soit en demandant un zoom entre deux cadres à l'intérieur d'une même image, soit lorsqu'il s'agit d'une Julia ou d'un Mandelbrot Incomplet, entre deux points sources. C'est très facile à faire, on est guidé par des instructions données par le programme. Pour gagner de la place, on peut demander que les images soient exécutées en petit format, par exemple un quart de l'écran. MandelTour n'assemble pas l'animation, il faut le faire via un programme comme Deluxe Paint 4 ou Animbuild.
Mais la fonction "Animation" a un autre intérêt, qui est tout simplement de faire de l'exploration automatique. Dans une zone critique, comme au voisinage de la frontière, on peut demander à MandelTour de calculer une dizaine d'images Julia et voir comment elles changent de forme. Pendant ce temps, on fait autre chose, et quand c'est fini, l'examen des images l'une après l'autre permet d'identifier le meilleur point source.
Il y a tout de même une limitation : on ne peut animer qu'entre deux cadres ou entre deux points sources d'une même image. Ceci limite évidemment l'amplitude du zoom que l'on peut faire.
Coloriage
L'intérêt et la lisibilité d'une image fractale dépendent énormément de la gestion des couleurs. MandelTour offre des possibilités de coloriage des images exclusives. Ceci d'ailleurs sans la moindre difficulté pour le débutant, car la méthode de coloriage par défaut est très performante, et elle donnera très souvent les meilleurs résultats en absolu. Nous savons déjà (voir l'article sur les fractales) que nous donnons à chaque pixel de l'écran une couleur qui dépend du nombre d'itérations qu'il a fallu effectuer pour que le module d'une fonction zn = zn-1^2 +C dépasse une certaine valeur. Chaque couleur représente donc une bande comprise entre deux courbes de niveau.
Dans la tache noire centrale de l'image du Mandelbrot pur, cette valeur n'a pas été atteinte et on s'est arrêté après un nombre arbitraire d'itérations, par exemple 1000. C'est un plateau. Charles Vassallo a une image très parlante pour présenter ce coloriage. Plus on est près de la tache centrale, plus on a dû faire d'itérations, plus on est dans une zone "chaude". A contrario, plus on s'éloigne, moins il a fallu faire d'itérations, on est dans une zone "froide". Il a donc choisi une palette de base qui va du bleu foncé au blanc en passant par le rouge, l'orange et le jaune.
Mais voilà, ce n'est pas si simple. Plus on s'approche de la tâche centrale, plus le nombre d'itérations grimpe vite, les lignes de niveau se resserrent, et une grosse partie de ces niveaux ne concerne qu'une bande assez étroite autour du plateau. Pour faire meilleur usage de la palette de couleurs, MandelTour s'arrange pour qu'il y ait à peu près autant de pixels dans chaque bande de couleur. Ceci améliore considérablement l'aspect des images.
Il y a encore mieux. Seulement, c'est assez complexe à décrire, alors que cela se comprend tout seul en faisant la manipulation, très clairement expliquée dans la documentation en couleurs. J'irai donc très vite. Pour économiser les couleurs et les réserver aux zones les plus intéressantes, ou pour donner à certaines zones l'aspect typique en zébrures, sans utiliser plus que les 32 ou 16 couleurs disponibles, on peut utiliser un mode de coloriage cyclique, qui va, par exemple, à l'aide de trois couleurs, colorer une zone en 15 zébrures, ce qui aurait autrement nécessité 12 couleurs additionnelles.
On arrive ainsi, avec les 32 couleurs du mode basse résolution, à obtenir des images comme on en trouve dans les ouvrages spécialisés et qui ont été calculées avec 256 couleurs ou plus. En outre, dans la zone "chaude" de l'image, une bande de couleurs représente un certain nombre de niveaux. MandelTour offre la possibilité de resegmenter cette bande en utilisant les couleurs précédentes. La figure 5 montre une image en 16 couleurs, sans recoloriage.

Figure 5

Figure 6
Il y a tout de même un point auquel il faut faire très attention : la séquence de recoloriage comporte de nombreuses étapes et on fait facilement des erreurs. Par exemple, les fonctions de recoloriage ne sont disponibles que juste après le calcul de l'image, car les données brutes sont stockées dans un fichier nommé "iter" qui est en RAM et qui est effacé dès qu'on lance un nouveau calcul.
Ceci fait que si, non satisfait du recoloriage d'une image, vous répondez non à la question "Faut-il sauver cette image ?", tout disparaît. Si vous répondez oui, l'image est sauvée mais elle écrase sur le disque toute image résultant d'une tentative précédente de recoloriage de la même image. Si donc vous voulez sauver plusieurs étapes successives dans un recoloriage, utilisez l'option "Voir" de la fenêtre de requête de recoloriage, qui fait disparaître la fenêtre de requête, et sauvez l'image au moyen d'un utilitaire de sauvegarde d'écran comme GraphicDump ou Grabbit.
Je n'ai trouvé dans tout cela qu'un (petit) piège : si vous demandez le calcul d'une image en haute résolution avec des couleurs foncées dans le bas de la palette, les fenêtres de requêtes ne sont plus lisibles. Mais encore une fois, le débutant n'a pas à s'effrayer de cela, le coloriage par défaut est vraiment très performant.
Enfin, il faut signaler l'existence d'une palette automatique qui colore l'image selon une quasi infinité de palettes choisies selon un mode partiellement aléatoire, qui défilent à vitesse réglable, que l'on arrête par la barre d'espace, laquelle permet alors de revenir sur les 20 dernières palettes qui ont défilé. De plus, il y a neuf répartitions de couleurs prédéfinies accessibles en pressant les touches de 1 à 9.
Ceci permet de trouver à coup sûr la palette qui optimisera vos images. Tout ceci est bien expliqué dans la documentation, et constitue un ensemble absolument unique dans les programmes de tracé de fractales sur Amiga.
A qui est destiné MandelTour ?
Toute la convivialité ainsi que le peu de considérations mathématiques dans la documentation, veulent-ils dire que MandelTour est réservé aux débutants ? Certainement pas. Je ne suis pas un expert en fractales ; néanmoins, je vais installer sur mon Amiga quelque chose qui me permette de traiter facilement les variables complexes, car il y a un moment dans la progression où pour comprendre ce qui se passe, il devient indispensable de faire des calculs sur des variables complexes.
Malgré cela, MandelTour restera pour moi un outil d'investigation très intéressant en matière de fractales de Mandelbrot et Julia. En effet, l'auteur a bien voulu insérer dans le programme, très discrètement pour ne pas nuire à sa convivialité, la possibilité de lire les paramètres d'une image et introduire des coordonnées au clavier lorsque l'approche à la souris n'est pas assez précise.
Retour sur le suraffichage
Si vous voulez utiliser MandelTour dans son suraffichage natif, procurez-vous auprès de Serge Hammouche sa disquette "*Utils#7*" qui comporte entre autres choses toutes les explications et les utilitaires nécessaires pour utiliser au mieux les possibilités de l'Amiga en suraffichage sans problèmes de cadrage, et recentrer instantanément les autres écrans lorsque vous y retournez alors que MandelTour fonctionne.
Sinon, vous avez la possibilité de modifier selon les instructions simples de la documentation le fichier d'initialisation de MandelTour pour que le programme s'ouvre en 320x256, et de refaire votre bibliothèque (après avoir sauvé l'originale, bien sûr). Ce n'est ni très long ni très difficile.
Et pour un peu j'allais oublier de signaler que MandelTour permet de réaliser des images jusqu'à une dimension de 1000x800 en 32 couleurs, à condition d'avoir assez de mémoire. On ne peut évidemment pas les afficher directement sur l'Amiga, mais grâce à un programme comme Mostra, vous pourrez les regarder en les faisant défiler au moyen des touches de curseur. Par contre, vous pourrez les faire sortir en 24x36 par exemple par des ateliers spécialisés (Serge Hammouche, les services de Tecsoft, les photos obtenues sont vraiment très belles).
Conclusion
Des critiques ? Non, pas vraiment. Étonnant, non ? Charles Vassallo a écrit MandelTour pour permettre à tout un chacun d'explorer les fractales de Mandelbrot et de Julia, en obtenant très vite des résultats encourageants, sans aucune connaissance des mathématiques, via une interface simple et conviviale. Ce qui n'exclut pas des explorations poussées et l'obtention d'images très sophistiquées.
Ce but a été parfaitement atteint, et, dans cette optique précise. MandelTour n'a pas d'équivalent dans le domaine public de l'Amiga. Ceci d'autant plus qu'il offre à l'utilisateur une possibilité de s'échapper dans le monde insolite et grandiose de l'espace à quatre dimensions, ce qui est également, sauf erreur de ma part, une rareté dans le DP Amiga.
Il n'est pas impossible que Charles Vassallo nous concocte dans un avenir assez indéfini une version offrant encore plus de possibilités. Mais comme ce n'est vraiment pas pour tout de suite, n'attendez pas pour commander chez Serge Hammouche les deux disquettes de MandelTour pour 70 FF. Vous ne le regretterez pas.
|
Nom : MandelTour. Développeur : Charles Vassallo. Genre : générateur de fractales. Date : 1991. Configuration minimale : Amiga OCS, 68000, 512 ko de mémoire. Licence : partagiciel. Prix : 70 FF. |
|












