 |
Vendredi 06 juin 2025 - 13:06 |
| Translate |
|
| Rubriques |
| Réseaux sociaux |
|
| Liste des jeux Amiga |
|
| Trucs et astuces |
|
| Glossaire |
|
| Galeries |
|
| Téléchargement |
|
| Liens |
|
| Partenaires |
|
| A Propos |
|
| Contact |
|
|
|
Note : ce document est issu de Comment Ça Marche et mis à disposition sous les termes de la licence Creative Commons.
Algèbre de Boole
Un processeur est composé de transistors permettant de réaliser des fonctions sur des signaux numériques. Ces transistors, assemblés entre eux forment des composants permettant de réaliser des fonctions très simples. A partir de ces composants il est possible de créer des circuits réalisant des opérations très complexes. L'algèbre de Boole (du nom du mathématicien anglais Georges Boole 1815 - 1864) est un moyen d'arriver à créer de tels circuits.
L'algèbre de Boole est une algèbre se proposant de traduire des signaux en expressions mathématiques. Pour cela, on définit chaque signal élémentaire par des variables logiques et leur traitement par des fonctions logiques. Des méthodes (table de vérité) permettent de définir les opérations que l'on désire réaliser, et à transcrire le résultat en une expression algébrique. Grâce à des règles appelées lois de composition, ces expressions peuvent être simplifiées. Cela va permettre de représenter grâce à des symboles un circuit logique, c'est-à-dire un circuit qui schématise l'agencement des composants de base (au niveau logique) sans se préoccuper de la réalisation au moyen de transistors (niveau physique).
Variable logique
Un ordinateur ne manipule que des données binaires, on appelle donc variable logique une donnée binaire, c'est-à-dire une donnée ayant deux états possibles: 0 ou 1.
Fonction logique
On appelle "fonction logique" une entité acceptant plusieurs valeurs logiques en entrée et dont la sortie (il peut y en avoir plusieurs) peut avoir deux états possibles : 0 ou 1.
En réalité ces fonctions sont assurées par des composants électroniques admettant des signaux électriques en entrée, et restituant un signal en sortie. Les signaux électroniques peuvent prendre une valeur de l'ordre de 5 Volts (c'est l'ordre de grandeur général) que l'on représente par un 1, ou 0 V que l'on représente par un 0.
Les portes logiques
Les fonctions logiques de bases sont appelées portes logiques. Il s'agit de fonctions ayant une ou deux entrées et une sortie :
- La fonction OU (en anglais OR) positionne sa sortie à 1 si l'une ou l'autre de ses entrées est à 1.
- La fonction ET (en anglais AND) positionne sa sortie à 1 si ses deux entrées sont à 1.
- La fonction OU EXCLUSIF (en anglais XOR) positionne sa sortie à 1 si l'une ou l'autre de ses entrées est à 1 mais pas les deux simultanément.
- La fonction NON (appelée aussi inverseur) positionne sa sortie à 1 si son entrée est à 0, et vice-versa.
Chronogramme
Un chronogramme est un diagramme montrant l'évolution des entrées et des sorties en fonction du temps. Voici par exemple ce à quoi pourrait ressembler un chronogramme de l'opérateur ET :
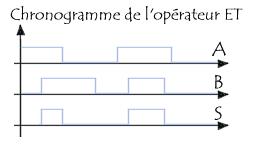
Ce chronogramme en un chronogramme idéal, en réalité les signaux électriques ne passent pas instantanément de 0 à 1, les pentes (ici verticales) sont obliques, et le traitement des entrées cause un retard sur les sorties :
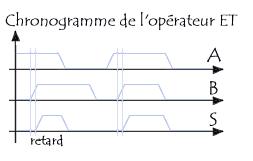
Expression algébrique
Le but de l'algèbre de Boole est de décrire le traitement de signaux sous forme d'expression algébrique. Comme nous l'avons vu, les signaux sont représentés par des noms de variables. Les fonctions logiques sont représentées par des opérateurs :
- La fonction OU est représentée par un plus : +
- La fonction ET est représentée par un point : .
- La fonction NON est représentée par une barre au-dessus de la variable inversée :
.
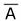Elle est parfois représentée par un / devant la variable inversée.
- La fonction OU EXCLUSIF est représentée par un plus encerclé :
.
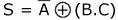
Table de vérité
Une table de vérité est un tableau permettant de décrire toutes les possibilités de sorties en fonction des entrées. On place donc les variables d'entrées dans les colonnes de gauche en les faisant varier de telle façon à couvrir l'ensemble des possibilités. La colonne (ou les colonnes si la fonction a plusieurs sorties) de droite décrit la sortie.
Voici par exemple les tables de vérités des portes logiques :
| Nom de la porte | Entrée | Sortie | |
| A | B | ||
| 0 | 0 | ||
| 0 | 1 | ||
| 1 | 0 | ||
| 1 | 1 | 0 | 0 |
| 0 | 1 | ||
| 1 | 0 | ||
| 1 | 1 | 0 | 0 |
| 0 | 1 | ||
| 1 | 0 | ||
| 1 | 1 | 0 | 0 |
| 0 | 1 | ||
| 1 | 0 | ||
| 1 | 1 | ||
Il est possible à partir de la table de vérité d'une fonction d'écrire l'expression algébrique de celle-ci. Soit la table de vérité suivante :
| Entrée | Sortie | |
| A | B | |
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 | |
La sortie vaut 1 lorsque A vaut 1 et B vaut 0, l'expression algébrique de cette fonction est donc :
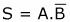
Prenons maintenant la table de vérité suivante :
| Entrée | Sortie | ||
| A | B | C | |
| 0 | 0 | 0 | |
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| 1 | 1 | 1 | |
La sortie vaut 1 lorsque :
- A vaut 0
- B vaut 1
- C vaut 0
- A vaut 1
- B vaut 1
- C vaut 0
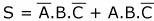
Les lois de composition
Les lois de composition sont des règles logiques qui permettent de simplifier l'écriture des expressions algébriques.
Associativité
(A.B).C est équivalent à A.(B.C)
(A+B)+C est équivalent à A+(B+C)
Absorption
A.(A+B) est équivalent à A
A+A.B est équivalent à A
Commutativité
A.B est équivalent à B.A
A+B est équivalent à B+A
Distributivité
A+(B.C) est équivalent à (A+B).(A+C)
A.(B+C) est équivalent à A.B+A.C
Idempotence
A.A est équivalent à A
A + A est équivalent à A
Identité
1.A est équivalent à A
0+A est équivalent à A
Inversion
A./A est équivalent à 0
A+/A est équivalent à 1
Nullité
0.A est équivalent à 0
1+A est équivalent à 1
Théorème de De Morgan
est équivalent à 
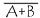est équivalent à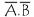 
Exemple de simplification d'expression
Soit la simplification suivante :
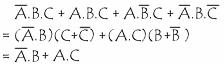
Circuits logiques
Représentation des portes logiques
La représentation conventionnelle des portes logiques est la suivante :
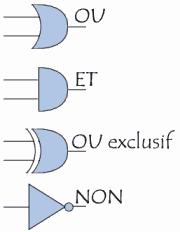
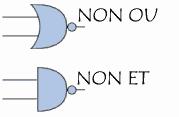
Réalisation de circuits logiques
On appelle circuit logique (ou circuit combinatoire) un ensemble de portes logiques reliées entre elles pour répondre à une expression algébrique. Il s'agit donc d'aller transcrire en schéma électrique (à l'aide des représentations ci-dessus) l'expression algébrique que l'on a simplifiée grâce aux lois de composition.
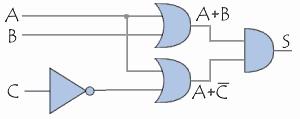
Par exemple l'expression algébrique
(A+B).(A+/C)sera schématisée comme suit :
Additionneurs
Un additionneur est un circuit capable de faire la somme de plusieurs nombres. Une addition met en oeuvre deux sorties :
- La somme, généralement notée S.
- La retenue, généralement notée R.
Additionneur de deux nombres de 1 bit
Pour une addition de deux nombres A et B de 1 bit, 4 combinaisons sont possibles, et le résultat occupe 2 bits : un bit pour la somme (S) et un pour la retenue (R).
Voici la table de vérité de cette fonction :
| Entrée | Sortie | ||
| A | B | ||
| 0 | 0 | ||
| 0 | 1 | ||
| 1 | 0 | ||
| 1 | 1 | ||
L'expression logique de cette fonction est donc :
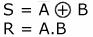
Le circuit peut donc être représenté selon le schéma électrique suivant :
|
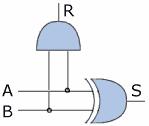
