Suivez-nous sur X

|
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z,
ALL
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
A propos d'Obligement

|
|
David Brunet

|
|
|
|
En Pratique : LightWave - Les opérations booléennes
(Article écrit par Laurent Belloni et extrait de Planet et d'Obligement 19 - janvier 2000)
|
|
Voyons donc de ce pas, l'une des possibilités les plus intéressantes que propose
le modeleur de LightWave : les opérations booléennes. Celles-ci sont en effet très, mais alors
vraiment très pratiques, voire nécessaires dès lors que l'on s'attaque à la
modélisation d'objets complexes. C'est-à-dire ceux qu'il serait quasiment impossible
de faire à l'aide d'autres outils... à moins de vraiment vouloir se compliquer la vie
et de perdre du temps pour rien, tout en se prenant la tête.
La théorie et le principe
Créer au milieu du XIXe siècle, l'algèbre booléen repose sur une loi dite "de
logique" ainsi que sur une "valeur de vérité". Ainsi, un élément est considéré comme
-vrai- ou -faux- (valeur de vérité). La "logique" intervient dans tout ce qui est
"loi d'absorption, d'addition, de commutativité, etc."
Ainsi, il ne s'agit ni plus ni moins de l'utilisation des fameux opérateurs logiques,
dont tout le monde a, ne serait-ce qu'une fois, entendu parlé dans sa vie : les fameux
"et", "ou", "et exclusif", "ou exclusif", etc.
Et dans la pratique, donc celle qui nous intéresse : celle de LightWave, il ne
s'agit ni plus ni moins de les utiliser (grâce à des outils expliqués plus bas) afin
de permettre de "réunir" deux objets A et B. Attention, ne pas prendre le mot "réunir" au
premier sens du terme, car dans le cas des opérations booléennes du modeleur de
LightWave, il s'agit plutôt de "mettre ensemble" afin de faire des opérations de
soustraction, d'addition, etc.
La méthode
Je vous parlais y'a pas si longtemps de cela de deux objets A et B. Eh bien, quoi que
vous fassiez avec les opérations booléennes, il y a toujours deux objets concernés ! Et
la chose à respecter est que chacun d'eux doit se trouver sur un calque différent !
Je vais de ce pas expliquer brièvement le fonctionnement des calques : en haut à droite de l'interface de LightWave (image
suivante) se trouve dix rangées de deux boutons chacune. Chaque rangée représente un calque,
et chaque calque est constitué d'un calque d'avant-plan, et d'un d'arrière-plan.
Dès qu'un calque ou plusieurs (avec la touche "Shift" enfoncée) est ou sont mis en avant-plan,
tous les objets présents dans ces calques sont visibles et éditables ! Alors
que lorsque qu'un ou plusieurs calques d'arrière-plan est ou sont sélectionnés (la
rangé du bas, donc), les objets présents dans ceux-ci sont visibles mais pas éditables.
L'avantage de l'utilisation des calques est de suite perceptible dans tout ce qui
concerne la modélisation, et dans le cas précis des opérations booléenes, l'utilisation
de ceux-ci sont nécessaires (et expliqué plus loin dans cet article).
Le but est que deux objets se confondent dans un espace 3D commun, afin que ceux-ci
interfèrent l'un à l'autre, et ce, de quatre manières différentes : l'addition, la
soustraction, l'union et l'intersection.
La seconde règle à respecter (après la nécessité d'utiliser deux objets sur deux calques)
est donc que ces 2 objets aient au minimum une partie dite "commune", c'est-à-dire qu'ils se confondent au moins partiellement
sur les deux plans que représentent les deux calques.
En fait, dans la théorie, cela n'est pas nécessaire... car on peut très bien "additionner" un objet à un autre sans pour autant
qu'il se confondent ne serait-ce que partiellement : ce serait en fait opérer à une simple jointure (un "join")... ce qui peut
s'avérer très utile dans certains cas ! Par contre, pour opérer une soustraction, il faut que les objets se confondent sinon cela
n'aurait aucun sens, ce serait donner un coup d'épée dans l'eau. ;)
La mise en oeuvre
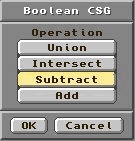
Pour accéder à toutes ces fonctions, il suffit de se rendre dans le panel "Tools", puis dans le sous-panel "Boolean" qui vous
proposera ces opérations sous le nom que je précise entre les parenthèses.
Important : dans toutes ces possibilités (et par rapport aux explications de celles-ci),
l'objet A est toujours en avant-plan, et le B en arrière-plan. Donc, à vous de faire
les bonnes sélections afin de ne pas faire le travail à l'envers... Pour représenter
mes explications, regardez les photos d'écrans, sachant que j'utilise toujours un cube
pour l'objet A et une sphère pour l'objet B.
L'addition (add)
Un objet A s'ajoute à un objet B, pour au final former un seul et unique objet
(fusion). La "matière" ou plutôt les faces qui se trouvent à l'intérieur du volume
obtenu sont conservées. Ce procédé (l'addition donc) est vraiment un assemblage pur
et dur des deux objets A et B. Sachez également que les surfaces (un ensemble de
polygones) ayant servi à former le nouvel objet conservent chacune leur nom respectif.
La soustraction (substract)
L'objet A enlève à l'objet B la "matière" qu'ils ont en commun. Il est à noter (et
c'est très important) que, l'objet A ne change pas (aucune matière ne lui est ni enlevé
ni ajouté), mais l'objet B lui, a subit une transformation...
En fait, l'objet A, le cube, n'a été utilisé que comme "outil" afin de "creuser"
l'objet B, la sphère. Il est également important de souligner que l'objet B
obtenu devient une nouvelle surface qui prend le nom qui a été attribué à A.
D'un point de vue pratique, la soustraction booléenne est sans doute la plus
importante, car grâce à elle il est permis d'évider n'importe quel objet possédant la
forme la plus biscornue ou délirante à l'aide d'un autre objet qui n'a par exemple
été créé que dans le but de servir d'outil. Il est donc très intéressant et pratique
de connaître parfaitement et de savoir utiliser au mieux cette méthode, car elle rend
très souvent des services (surtout dans la création d'objets complexes).
L'union (union)
Dans le principe, l'union booléenne peut être comparée avec l'addition précédemment
expliquée. L'union agit de la même manière que l'addition, mais les faces se trouvant
à l'intérieur du volume obtenu sont éliminées (à l'inverse de l'addition). Chaque
surface conserve son nom.
L'intersection (intersec)
Imaginez totalement l'inverse de l'union et vous aurez tout compris du premier coup.
En fait, seule reste la matière commune aux deux objets, tout le reste est simplement
éliminé. Pour cette opération aussi, chaque surface conserve son nom.
Note : toutes ces opérations booléennes ne sont qu'applicables qu'avec des formes 3D.
Seule l'addition booléenne est particulière dans le sens ou rien n'empêche
d'additionner un objet 2D avec un autre objet en 2D ou 3D. Ce qui la différencie
un peu plus de l'union booléenne !
Problèmes ?
Dans certaines manipulations, il peut arriver que le modeleur de LightWave vous
montre un beau message d'erreur à la place de faire ce dont vous lui avez demandé.
Cela arrive assez souvent en raison de ce que l'on pourrait appeler "une mauvaise
interprétation des faces des objets A et B"...
Pour remédier à ce problème qui n'apparaît heureusement que très rarement, l'unique
solution que j'ai trouvée est d'ajouter des faces à l'un des deux objets ou d'éviter
que des points d'un objet ne se confondent trop précisément avec des points de l'autre
objet... c'est-à-dire de déplacer très légèrement soit un des deux objets, soit uniquement
le ou les quelques points incriminés.
|