Suivez-nous sur X
|
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z,
ALL
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
A propos d'Obligement
|
|
David Brunet
|
|
|
|
En pratique : Coloriage des images de Mandelbrot
(Article écrit par Charles Vassallo et extrait d'Amiga News - mai 1994)
|
|
Depuis le tout début, l'une des préoccupations favorites des programmeurs et des
utilisateurs de l'Amiga a été de calculer des images de l'ensemble de Mandelbrot.
Cet article présente l'état de mes réflexions après la refonte de mon propre
programme (MandelTour) pour les nouvelles machines 256 couleurs.
Coloriage cyclique et par histogramme
Les images de Mandelbrot ne sont qu'un cas particulier d'un problème plus
général : il s'agit de traduire en couleurs l'association d'un nombre N
à chacun des pixels de l'écran, c'est-à-dire de visualiser une fonction N(x,y)
des coordonnées x,y de ces pixels. La quasi-totalité des programmes Mandelbrot met en
oeuvre un coloriage cyclique.
Dans la version la plus simple, on associe la couleur 0 à N=0 et on se déplace d'un
rang dans la gamme des couleurs disponibles chaque fois que N augmente de 1, jusqu'à
ce qu'on arrive au bout, auquel cas on revient sur la première couleur. On ajoute
généralement deux autres ingrédients à la recette : on peut choisir une autre couleur
pour le démarrage ("l'offset", en mauvais français), et on peut convenir de ne
passer d'une couleur à la suivante que si N augmente de 2, de 3... (le "skip" ou
le "color increment"). Un résultat typique se voit sur la figure 1 : suffisamment
spectaculaire pour accrocher les profanes, et plutôt décevant quand on sait ce
qu'on peut obtenir avec le même coin de l'ensemble de Mandelbrot, en s'y prenant
mieux avec la répartition des couleurs (figure 2).
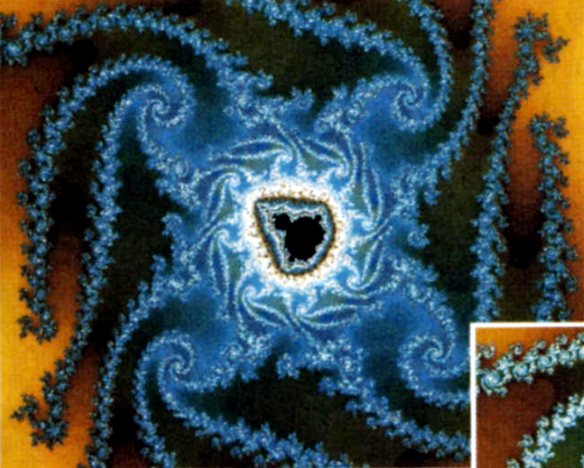Figure 1
Figure 2
Si on ne veut pas de ce coloriage cyclique, il faut bien préciser d'une façon ou
d'une autre la règle de passage entre le nombre N et la couleur correspondante.
Il est impossible de se fixer une règle a priori, valable pour toute image.
Comme on connaît la valeur maximale de N (ce NMAX est l'un des paramètres du
calcul des images de Mandelbrot), on pourrait envisager de découper l'intervalle (0,NMAX)
en autant de tranches égales qu'il y a de couleurs disponibles, en affectant la
première couleur à la première tranche, la deuxième à la deuxième tranche et ainsi de suite.
On obtiendrait ainsi un coloriage "scientifique" qui renseignerait immédiatement sur
la valeur de N au simple vu de la couleur du pixel, avec une "échelle linéaire"
(c'est-à-dire que N est en gros proportionnel au numéro de la couleur dans la palette),
mais avec des résultats inacceptables sur le plan artistique.
Dans une image Mandelbrot typique, par exemple calculée avec NMAX=1000,
les nombres N partent d'une valeur minimum beaucoup plus faible, disons 30,
et la plupart des points de l'image se situent tout près de ce minimum. Pour éviter
que ces points ne se traduisent par de grandes zones uniformes dans l'image. Il est
très important de bien distinguer quand N varie d'une unité près de ce minimum :
il faut alors des "tranches" de largeur unité. A l'opposé, très peu de points montent
jusqu'au maximum et il faut que les "tranches" pour N élevé soient très larges.
Il faut donc tailler sur-mesure la loi de traduction entre N et la couleur.
Mais comme on ne connaît pas le minimum d'avance, il faut nécessairement commencer
par faire tout le calcul en mémorisant tous les N, puis examiner ces N et décider en
conséquence, puis enfin faire le coloriage définitif.
Cela complique un peu la programmation, mais pas de manière excessive. Évidemment, on perd
quelques secondes pour l'analyse des N et la recoloration, mais, après un calcul cent
ou mille fois plus long, ce retard supplémentaire ne devrait pas être insupportable.
Bien entendu, il importe que cette traduction en couleurs soit automatique. On ne
peut pas sérieusement reprendre l'option proposée par MandelVroom (sans doute le premier
programme autre que MandelTour qui se soit sérieusement penché sur le problème), qui
consistait ni plus ni moins à faire l'opération à la main, N par N. La technique
employée dans MandelTour est basée sur l'analyse de l'histogramme des N. On
peut l'expliquer schématiquement de la manière suivante :
1. On commence par dresser l'histogramme, c'est-à-dire qu'on remplit
un tableau HISTO(N) pour N=0, ...NMAX, indiquant combien il y a de pixels sur
l'image pour chacune des valeurs de N possibles. Bien entendu, la somme des
HISTO(N) doit redonner le nombre de pixels de l'écran, c'est-à-dire le nombre TOTAL
des pixels à colorier.
2. On va essayer de donner le même poids aux diverses couleurs disponibles,
en principe 256 pour les machines AGA. Toutes les couleurs devraient être représentées par
le même nombre de pixels sur l'écran, c'est-à-dire le nombre QUOTIENT=TOTAL/nombre de
couleurs à répartir. On attribuera ainsi la première couleur aux premiers nombres N,
c'est-à-dire N=0,1,2... jusqu'à ce que le nombre correspondant de pixels HISTO(0)+HISTO(1)+HISTO(2)...
soit à peu près égal à QUOTIENT. Évidemment, on n'a jamais l'égalité exacte.
3. On a ainsi réglé le sort de la première couleur et des premiers N.
On soustrait le nombre de pixels correspondant de TOTAL (qui reste ainsi le
nombre total de pixels non coloriés) ; on enlève 1 au nombre de couleurs à répartir, et
on recommence la deuxième étape pour les N suivants, et ainsi de suite, jusqu'à ce
qu'on arrive à TOTAL=0.
4. On a ainsi dressé la table de traduction, qui définit la couleur associée à
chaque N. Il faut enfin relire les fichiers des N pour chaque pixel, traduire ce N par
une couleur au moyen de cette table, et faire la recoloration réelle de l'image.
Les complications en 256 couleurs
L'arrivée des machines AGA a ouvert un nouveau monde aux coloristes. Dans le cercle
des aficionados, on savait que les belles images de Mandelbrot exigeaient la haute
résolution et on avait particulièrement souffert de la limitation à 16 couleurs -
à témoin les complexités du menu "recoloration" du premier MandelTour.
En réalité, il y avait l'échappatoire possible de faire des pseudo-couleurs par mélange
optique - "dithering", disent les grand-bretons, ou "tramage" en français.
Cette voie a été suivie dans le programme LyapTour consacré aux fractales de Lyapounov
avec des résultats très convaincants, mais il n'y avait pas eu de suite pour
l'ensemble de Mandelbrot. L'arrivée des machines 256 couleurs a relégué cette
possibilité aux oubliettes.
Curieusement, il apparaît un problème inattendu : après avoir souffert d'un "trop peu",
on a tout à coup trop de couleurs ! En effet, l'application directe de la méthode
précédente avec 256 couleurs ne conduit pas à de bonnes images, principalement parce que
les premières cases de l'histogramme sont de beaucoup les plus remplies ;
HISTO(N) s'écroule très vite quand N augmente. L'effet est que le TOTAL des pixels non affectés
diminue très vite alors qu'il reste encore beaucoup de couleurs à attribuer, conduisant
à des QUOTIENT(s) très petits. Ces couleurs sont donc représentées par très peu de points
sur l'écran ; au mieux cela ne se voit pas - et la couleur est donc inutile - et au pire,
on obtient un effet de poussière désagréable sur l'image.
Il faut donc empêcher QUOTIENT de descendre trop bas, en lui fixant un minimum.
Cela doit se faire de manière interactive : le minimum convenable pour une image ne
convient pas forcément à une autre.
Un effet secondaire est qu'on ne va pas utiliser toutes les couleurs disponibles. Dans les
faits, depuis que je travaille sur l'ensemble de Mandelbrot en 256 couleurs, je n'ai jamais
rencontré d'image qui ait vraiment besoin de plus d'une centaine de couleurs.
Cela a des conséquences sur l'utilitaire de palette qu'on va utiliser pour régler les teintes :
si une image n'emploie que 50 couleurs, c'est du gaspillage d'offrir de quoi ajuster
les 206 autres !
D'autres contraintes apparaissent à cause même du système 3.0.
Intuition utilise une bonne douzaine de couleurs pour habiller ses fenêtres et obtenir
le fameux aspect 3D. Il vaut mieux ne pas modifier ces couleurs, ou, si on le fait,
il faut respecter leurs significations. A vrai dire, cela existait depuis le 2.0,
mais vu le petit nombre des couleurs disponibles, il n'était guère question de respecter
ces conventions dans des programmes de coloriage. Avec la pléthore de couleurs des
nouvelles machines, il serait dommage de s'en priver ; la présentation du programme
gagne considérablement en élégance.
Il faudra donc clairement distinguer les couleurs réservées au système et celles qui
sont disponibles pour les images. L'utilitaire de palette devra permettre d'accéder à
ces deux catégories, mais en empêchant l'utilisateur de les confondre. La figure 3
donne une idée de la solution proposée dans MandelTour ; la palette ne présente que
les couleurs réellement utilisées, et les couleurs réservées par Intuition (les premières)
apparaissent dans des plots plus petits que les couleurs de l'image.
Figure 3
Il y a d'autres exigences auxquelles l'utilitaire de palette doit répondre. Un problème
tout bête est de masquer le moins possible de surface écran, afin qu'on puisse suivre
sur l'image l'effet de l'action menée sur la palette elle-même ; le bouton "zoom" offert
par les systèmes 2.0 et 3.0 ne permet pas ce suivi en temps réel. Bien entendu, ce
problème devient très difficile pour une palette complète de 256 couleurs sur un écran
basse résolution, surtout si on ne veut pas sacrifier la lisibilité.
Une autre difficulté spécifique des images AGA vient du grand nombre des couleurs - même
si on n'utilise pas tout, on en prend quand même beaucoup plus que les 32 de l'époque
héroïque. Une palette typique pour une image Mandelbrot se compose d'une suite de dégradés. A
première vue, faire un dégradé ne demande pas trop d'efforts : on règle les composantes
RVB ou CSI des deux couleurs extrêmes, puis on clique sur un bouton "Dégradé". C'est
tout de même plus simple que l'ajustage des couleurs une à une.
Dans la pratique, quand on a cinq ou six dégradés enchaînés et qu'on doive les reprendre
en tout ou partie parce que, peut-être, leurs sommets ne sont pas placés au mieux dans
la palette, ou que, peut-être, d'autres couleurs pourraient être plus satisfaisantes (et
bien évidemment, il faut faire l'expérience à chaque fois pour en avoir le coeur net),
ce cycle devient rapidement fastidieux et on se prend à rêver d'une palette plus intelligente
qui saurait réduire ces opérations à quelques coups de souris. Pour l'heure, autant que
je sache, seul MandelTour propose des réponses à tous ces problèmes de convivialité.
D'autres rendus pour les images
En prime, le stockage temporaire des N(x,y) offre quelques autres possibilités :
on peut se livrer à quelques manipulations sur ces nombres avant de les traduire en couleurs.
Cela permet d'obtenir d'autres types d'images. Quelques voies sont abordées dans MandelTour,
mais on peut sûrement en imaginer d'autres. Les figures 4 et 5 donnent deux exemples.
La figure 4 montre un estompage, à partir d'une opération d'un moyennage partiel
entre un pixel et ses voisins. La figure 5 est une application d'une détection de contour
entre plages à N constant. On peut aussi renforcer le contraste local, pour mieux faire
ressortir les filaments ; cette technique a été mise en oeuvre dans la figure 2.
Figure 4
Figure 5
|
