 |
Dimanche 21 décembre 2025 - 04:37 |
| Translate |
|
| Rubriques |
| Réseaux sociaux |
|
| Liste des jeux Amiga |
|
| Trucs et astuces |
|
| Glossaire |
|
| Galeries |
|
| Téléchargement |
|
| Liens |
|
| Partenaires |
|
| A Propos |
|
| Contact |
|

|
|
Comme beaucoup d'entre vous le savent, le C est un très bon langage de haut niveau pour écrire des applications rapides. Cependant, il n'y a généralement que quelques endroits dans le code du programme où cette vitesse est critique, c'est-à-dire importante du point de vue de l'utilisateur. En général, le traitement des entrées de l'utilisateur à travers l'interface d'une application ne fait pas partie de ces points critiques. On pourrait alors se demander si l'on ne pourrait pas construire l'interface à l'aide d'un outil de création interactif tel que Helm ou CanDo, écrire les parties critiques en termes de vitesse en C, puis combiner les deux ? La logique derrière cela est qu'une interface est plus facile à construire avec un outil de création qu'en C. Même si l'on utilise une trousse d'outils de création d'interface qui écrit le code C pour vous, il est parfois déroutant d'ajouter la gestion des événements.
Dans cet article, je vous montre une façon d'utiliser un outil de création pour construire une interface (alias "frontend", frontal) à une application C dont la vitesse est critique. Il n'y a pas beaucoup d'applications qui sont aussi intensives en mathématiques à virgule flottante que celles qui tracent l'ensemble de Mandelbrot et les ensembles de Julia. J'ai écrit les calculs de base pour une telle application en SAS/C 6.50 et j'ai ensuite ajouté une interface utilisateur conçue en CanDo 2.51. Pour souligner les avantages en termes de vitesse de l'écriture des calculs en C par rapport au langage de script de CanDo, j'ai également écrit les calculs en CanDo afin de pouvoir comparer la vitesse.
L'ensemble de Mandelbrot et les ensembles de Julia
Pour ceux d'entre vous qui ne connaissent pas l'ensemble de Mandelbrot et les ensembles de Julia (où étiez-vous ces dix dernières années, sous un rocher ?), je vais vous donner une brève explication. L'ensemble de Mandelbrot est une entité mathématique connue sous le nom de fractale. Il peut être défini de façon semi-formelle comme l'ensemble de tous les points, ci, du plan complexe tels que la valeur de z dans la formule d'itération zn+1=zn2+ci reste bornée lorsque n s'approche de l'infini pour une valeur initiale de z (z0) de 0+0i. On peut montrer que si la distance de z à l'origine dépasse jamais deux, alors la valeur de z s'approche de l'infini lorsque n s'approche de l'infini et n'est donc pas bornée.
Les ensembles de Julia sont également des fractales et sont similaires à l'ensemble de Mandelbrot. Cependant, il existe un nombre infini d'ensembles de Julia alors qu'il n'y a qu'un seul ensemble de Mandelbrot. Il y a un ensemble de Julia pour chaque valeur de ci dans le plan complexe. L'ensemble de Julia pour une valeur particulière de ci est l'ensemble de tous les points, z, du plan complexe tels que la valeur de z dans la formule d'itération zn+1=zn2+ci reste bornée lorsque n s'approche de l'infini.
Voilà pour les définitions. Si vous avez déjà vu des graphiques de Mandelbrot ou de l'ensemble de Julia, vous savez que les points qui composent l'ensemble ne sont généralement pas le principal point d'intérêt ; ce sont les points qui entourent immédiatement l'ensemble qui le sont. En général, les points appartenant à l'ensemble sont tous d'une seule couleur et les points voisins sont colorés différemment en fonction du nombre d'itérations nécessaires pour que la distance du point z par rapport à l'origine dépasse deux. On obtient ainsi une image comme celle de la figure 1, qui représente l'ensemble de Mandelbrot.
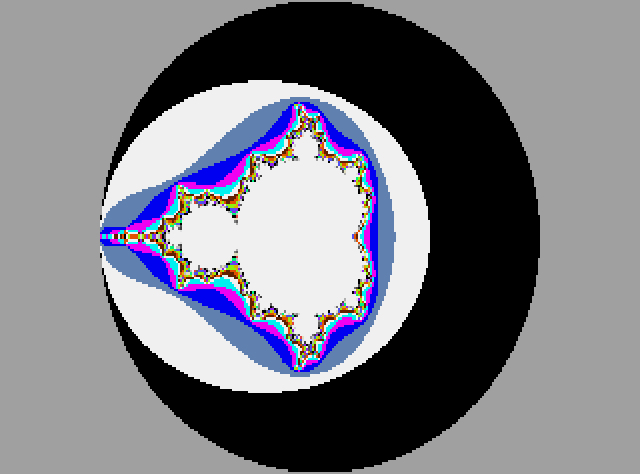
Figure 1 : ensemble de Mandelbrot (Dwell maximum=31)
Mon programme, CanDoMJ, permet à l'utilisateur de fixer le temps d'arrêt maximal à 15, 31, 63 ou 127 via un menu. Plus cette valeur est grande, plus le tracé sera précis, mais plus il faudra de temps pour calculer les points proches de l'ensemble et dans l'ensemble. Jetons maintenant un coup d'oeil au programme CanDoMJ. Il est présenté dans le listing 1.
Le deck CanDoMJ
Le deck CanDoMJ est composé de deux cartes : MJSettings et MJPlotPic. La première est l'interface utilisateur principale où l'on peut entrer divers paramètres liés au type de graphique à générer. Cette carte est la première à apparaître lorsque le programme commence son exécution. La seconde est utilisée pour tracer réellement l'ensemble de Mandelbrot ou de Julia.
La carte MJSettings
Cette carte est présentée dans la figure 2. Elle se compose de six champs de texte, d'un bouton Image, de deux boutons Texte et d'un menu contenant quatre éléments de menu. Certains de ces éléments sont également associés à des sous-éléments. La carte comporte également des scripts BeforeAttachment et AfterAttachment ainsi qu'une routine locale appelée DrawMJPic.
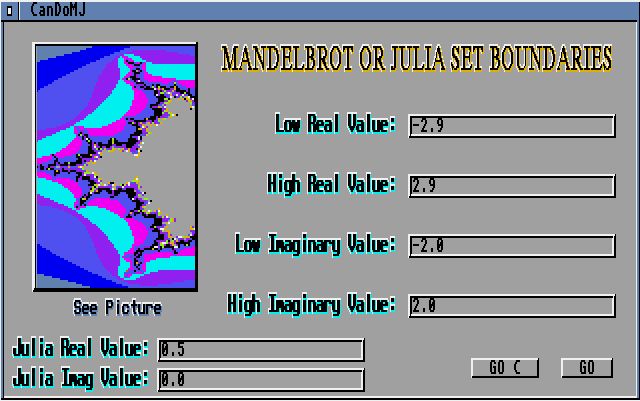
Figure 2 : Interface de CanDoMJ (carte MJSettings)
Ce script s'exécute juste avant l'affichage de la carte. Il vérifie si c'est la première fois que le script a été exécuté (Invocation=0 ; toutes les variables non initialisées ont une valeur par défaut de 0) et, si c'est le cas, il définit des valeurs par défaut pour le Dwell maximum, la résolution du tracé et le type de tracé. Ces valeurs par défaut peuvent être modifiées par des sélections de menu. La valeur de l'Invocation est fixée à un afin que ces valeurs par défaut ne soient plus définies pendant l'exécution du programme.
Le script AfterAttachment pour la carte MJSettings
Ce script supprime d'abord la coche de toutes les sous-rubriques du menu, puis ajoute une coche aux sous-rubriques appropriées, déterminées par les valeurs actuelles de Max Dwell, Resolution et Plot Type. Cela est nécessaire puisque CanDo met automatiquement des coches sur les sous-items dont la propriété Checked est définie au moment de la conception. Ensuite, la valeur du premier argument transmis à la carte, Arg1, est vérifiée. Si elle est égale à "Reset", les six champs de texte sont remplis avec les valeurs actuelles des six variables. Si cela n'est pas fait, CanDo remplira automatiquement les champs avec les valeurs par défaut spécifiées lors de la conception. Enfin, tout le texte de la carte (voir la figure 2) est affiché.
Les champs de texte
Les six champs de texte sont nommés LowReal, HighReal, LowImag, HighImag, JReal et JImag. Les quatre premiers champs (sur le côté droit de la carte) servent à saisir des nombres à virgule flottante qui définissent la région rectangulaire du tracé sur le plan complexe. Les valeurs par défaut de ces champs sont respectivement -2,9, 2,9, -2,0 et 2,0. Les champs de texte JReal et JImag (dans le coin inférieur gauche de la carte) servent à saisir des nombres à virgule flottante qui définissent la valeur complexe, ci, utilisée lors du tracé d'un ensemble de Julia. Les valeurs par défaut sont 0,5 et 0,0, respectivement.
Les six champs de texte ont un script d'événement OnRelease qui active simplement le champ suivant dans la séquence. Ceci élimine le besoin d'activer chaque champ en cliquant avec la souris entre les entrées. Sachez que les champs de texte permettent la saisie de n'importe quel caractère alphanumérique. Il serait bien qu'INOVAtronics ajoute un objet de champ de saisie masqué à CanDo ou, mieux encore, qu'elle fournisse un événement KeyPress pour les objets de champ. Cette dernière fonctionnalité permettrait d'exécuter un script chaque fois que l'utilisateur appuie sur une touche pendant qu'il saisit du texte dans un champ. Cela permettrait au programmeur de filtrer les entrées de l'utilisateur.
Les boutons Image et Texte
Le bouton Image est nommé "SeeMJPic" et apparaît sur le côté gauche de la carte. En cliquant sur ce bouton, le dernier graphique généré s'affiche. L'image de ce bouton est une brosse nommée "CanDoMJButton.br". Le script OnRelease de ce bouton exécute la routine DrawMJPic en lui passant l'argument "SEE".
Les deux boutons Texte s'appellent GOC et GO. Ils apparaissent dans le coin inférieur droit de la carte. Le premier est utilisé pour générer un tracé en appelant un programme C ; le second est utilisé pour générer le même tracé en utilisant le code CanDo. Les scripts OnRelease de ces boutons exécutent la routine DrawMJPic, en passant les arguments "GOC" et "GO", respectivement.
La routine DrawMJPic
Cette routine extrait le texte de chaque champ de texte de la carte et assigne leurs valeurs à six variables globales nommées de manière appropriée. Elle active ensuite la carte MJPlotPic, en lui transmettant l'argument qui a été transmis à la routine elle-même. Le contenu des champs doit être assigné aux variables parce que la carte MJPlotPic ne sait rien des champs de la carte MJSettings mais peut accéder aux variables globales.
Le menu PlotInfo
La carte MJSettings possède une structure de menu appelée "PlotInfo" qui contient quatre éléments de menu. Certains de ces éléments de menu ont des sous-éléments. La structure du menu ressemble à ceci :
PlotInfo Max Dwell 15 31 63 127 Resolution 1 2 4 8 Plot Type Mandelbrot Julia Default Settings |
Chaque élément ou sous-élément de menu sélectionnable est associé à une touche de raccourci. Ils sont présentés dans les sections de définition des objets de menu dans le listing 1.
Les sous-éléments de menu sous "Max Dwell" sont mutuellement exclusifs ; un seul élément peut être actif à la fois. Une coche apparaît à côté de la valeur sélectionnée. Cependant, CanDo ne gère pas automatiquement les sous-éléments de menu mutuellement exclusifs. Il vérifie l'élément sélectionné, mais il ne supprime pas la coche des autres éléments. Cela doit être fait par le programmeur. Comme vous pouvez le voir dans les scripts Occurred des sous-éléments (nommés MD15, MD31, MD63 et MD127), non seulement la valeur de Max Dwell est définie, mais les sous-éléments non sélectionnés voient leur coche supprimée à l'aide de la commande SetObjectState. La même procédure est utilisée pour les sous-items "Resolution" et "Plot Type" (Type de Tracé). Pour que les coches apparaissent et disparaissent correctement, assurez-vous que la propriété "Checkmark" (Coche) des sous-éléments est définie au moment de la conception (voir figure 3).
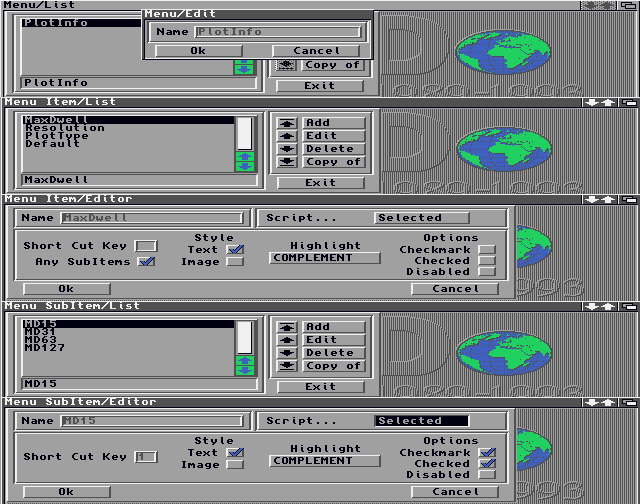
Figure 3 : Requêtes de création de menu
La valeur de la Résolution peut être 1, 2, 4 ou 8. Lorsque la valeur de la Résolution est N, alors une zone de NxN pixels sera dessinée à l'écran pour chaque point calculé dans l'ensemble de Mandelbrot ou de Julia. Ainsi, si la Résolution est égale à 4, un bloc de 4x4 pixels sera coloré pour chaque point calculé. Cela permet de générer des tracés grossiers mais rapides avant de tracer réellement avec une résolution de 1. La figure 4 montre un tracé de l'ensemble de Julia avec une résolution de 4.

Figure 4 : ensemble de Julia avec Resolution=4
Lors de la création d'une structure de menu dans CanDo, plusieurs niveaux de requêtes doivent être renseignés pour créer les éléments et sous-éléments du menu. Ces différentes requêtes sont présentées ensemble dans la figure 3. Il peut être difficile de s'y retrouver dans la création d'une structure de menu complexe. J'aimerais voir ces requêtes combinées en une seule requête bien conçue.
La carte MJPlotPic
Cette carte consiste en une fenêtre 320x200 32 couleurs sans aucun objet de fenêtre système. Ainsi, la carte semble totalement vide. Cependant, la carte possède un bouton de zone appelé "NewRange" et une structure de menu appelée "Options". La carte comporte également un script "AfterAttachment".
Le script AfterAttachment pour la carte MJPlotPic
Ce script vérifie d'abord la valeur de Arg1. Si elle est égale à "GO", un tracé est généré avec le code CanDo. S'il est égal à "GOC", un tracé est généré à l'aide du programme C, CanDoMJC. S'il est égal à "SEE", le dernier tracé généré est affiché.
Si le code CanDo doit être utilisé pour générer un tracé, plusieurs variables sont initialisées, et un tracé de l'ensemble de Mandelbrot ou de l'ensemble de Julia est créé en fonction de la valeur de Plot Type. Je vous laisse le soin de suivre le code et de voir comment il implémente les formules données au début de cet article. Plusieurs références sont également données à la fin de cet article.
Si le programme C, CanDoMJC, doit être utilisé pour générer un tracé, une chaîne de commande AmigaDOS est construite à l'aide de plusieurs opérations de concaténation de chaînes de caractères, puis exécutée à l'aide de la commande DOS. La commande finale ressemblera à quelque chose comme ceci :
RCF:C_Progs/CanDoMJC/CanDoMJC 3811064 31 2 -2.9 2.9 -2.0 2.0 J -0.5 0.0 |
Le paramètre 0 (vu par le programme C) est le chemin et le nom du fichier du programme C. Le premier paramètre est l'adresse mémoire de la structure de données "Window" de la carte "MJPlotPic". Cette adresse est disponible par le biais de la variable système CanDo, WindowAddress. Les deuxième et troisième paramètres sont les valeurs de Max Dwell et de Resolution. Les quatrième à septième paramètres sont les valeurs représentant l'étendue du tracé. Le huitième paramètre est le Plot Type, M ou J. Enfin, les neuvième et dixième paramètres sont les parties réelle et imaginaire de la valeur ci utilisée dans les tracés de l'ensemble Julia. Le programme C est décrit ci-dessous.
Si l'utilisateur veut juste voir le dernier graphe généré, alors le fichier RAM:CanDoMJPic, qui est utilisé pour stocker le dernier graphe (voir ci-dessous), est chargé dans le tampon MJPic et affiché. Sachez que si aucun tracé n'a encore été généré, le fichier RAM:CanDoMJPic n'existera pas. Dans ce cas, CanDo affichera automatiquement une requête de fichiers pour que l'utilisateur puisse faire une sélection. De plus, si vous utilisez TheMultiBinder pour créer un outil à partir de ce deck, n'incluez pas CanDoMJPic pendant le processus de liaison. Si vous le faites, TheMultiBinder ajoutera l'image actuelle de ce fichier au deck relié. Cela empêche le programme de charger le fichier à chaque fois qu'il doit être affiché, et donc de montrer toujours la même image.
Le bouton de la zone NewRange
Ce bouton permet à l'utilisateur de cliquer sur le bouton gauche de la souris à n'importe quel endroit de l'écran, de faire glisser un rectangle, puis de relâcher le bouton. Ce faisant, une nouvelle plage de traçage est définie en fonction des limites du rectangle. Le bouton a une taille de 320x200 pixels et n'a ni surbrillance ni bordure. Par conséquent, il couvre toute la carte et est invisible. La seule raison de son existence est de détecter les clics et les mouvements du bouton de la souris. Ni l'objet fenêtre ni la carte ne peuvent gérer les événements de la souris. Ainsi, la carte entière doit être couverte par un bouton de zone invisible. Le bouton comporte trois scripts pour lui permettre de fonctionner correctement : OnClick, OnDrag et OnRelease. OnClick s'exécute lorsque le bouton gauche de la souris est enfoncé, OnDrag s'exécute lorsque la souris est déplacée tout en maintenant le bouton gauche de la souris enfoncé, et OnRelease s'exécute lorsque le bouton gauche de la souris est relâché.
Le script OnClick détermine l'emplacement actuel de la souris à partir des variables système MouseX et MouseY. En outre, la largeur et la hauteur du rectangle sont fixées à 0, le mode de dessin est fixé à "COMPLEMENT" et un rectangle initial est dessiné. Lorsque la souris est déplacée, le script OnDrag s'exécute sans cesse. Il dessine d'abord un autre rectangle par-dessus le rectangle précédemment dessiné. Comme le mode de dessin est "COMPLEMENT", le rectangle précédent disparaît. Ensuite, la largeur et la hauteur du rectangle sont mises à jour et un autre rectangle est dessiné. Cela donne l'impression à l'écran que le rectangle est élastique et qu'il s'étire en fonction des mouvements de la souris. Ce processus se poursuit jusqu'à ce que le bouton gauche de la souris soit relâché. Le script OnRelease dessine d'abord un dernier rectangle pour effacer le dernier rectangle dessiné. Il met ensuite à jour les plages réelles et imaginaires du tracé en fonction des limites du rectangle. Ensuite, l'image courante est déplacée dans le tampon MJPic et sauvegardée dans le fichier RAM:CanDoMJPic afin qu'elle puisse être rappelée plus tard si nécessaire.
Enfin, la carte MJSettings est activée, en passant un argument de "Reset" pour que les champs des limites du tracé soient mis à jour. Sachez que le code prévoit uniquement que le rectangle soit dessiné du haut à gauche au bas à droite. Si vous essayez de créer le rectangle d'une autre manière, les valeurs hautes et basses seront interchangées, ce qui produira des tracés inversés ou à l'envers.
Le menu Options
La carte MJPlotPic possède une structure de menu appelée "Options" qui contient trois éléments de menu. La structure du menu ressemble à ceci :
Options Save Picture Set Colors To Settings |
Chaque élément de menu est associé à une touche de raccourci. Ils sont présentés dans les sections de définition des objets du menu dans le listing 1.
Lorsque l'option "Save Picture" (Enregistrer l'Image) est sélectionnée, une requête de fichiers s'affiche, permettant à l'utilisateur de sélectionner un nom de fichier vers lequel enregistrer le tracé actuel. Ceci est utile si vous souhaitez déplacer l'image dans un logiciel de dessin ou de traitement d'images pour la modifier.
Lorsque l'option "Set Colors" (Paramétrer les Couleurs) est sélectionnée, la carte ChangePalette du deck ColorChange s'ouvre en tant que requête, permettant à l'utilisateur de modifier les couleurs du tracé (voir figure 5).
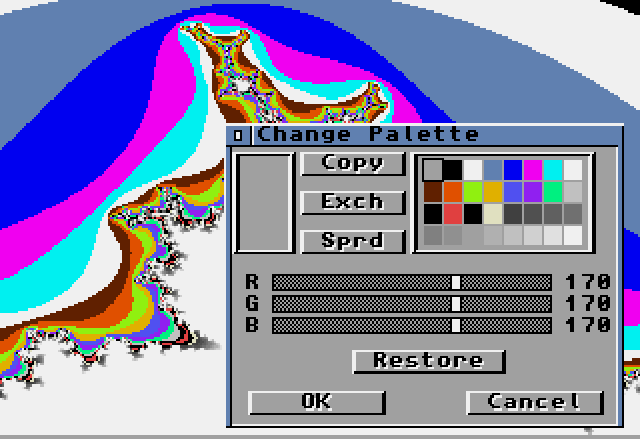
Figure 5 : carte MJPlotPic avec la requête de changement de couleur
Le programme C CanDoMJC
Ce programme est constitué de deux fichiers sources : un fichier d'en-tête nommé "CanDoMJC.h" et le fichier principal nommé "CanDoMJC.c". Le premier est présenté dans le listing 2, le second dans le listing 3.
CanDoMJC.h, qui est inclus par CanDoMJC.c, inclut plusieurs fichiers d'en-tête du système, définit certaines variables macro, et déclare certaines structures utiles. Il contient également deux fonctions pour ouvrir et fermer les bibliothèques système Intuition et Graphics.
CanDoMJC.c contient deux fonctions en plus de la fonction principale obligatoire. La première s'appelle "MJPlot". Elle est utilisée pour tracer l'ensemble de Mandelbrot ou de Julia demandé. Si vous êtes familier avec la programmation en C, vous verrez que le code est très similaire au code de traçage de CanDo dans le script AfterAttachment pour la carte MJPlotPic. En fait, les algorithmes sont exactement les mêmes et produiront des tracés identiques pour les mêmes paramètres. La deuxième fonction supplémentaire s'appelle "SetComplexRange" et remplit simplement une structure de données ComplexRange avec quatre valeurs à virgule flottante passées comme paramètres à la fonction.
La fonction principale déclare plusieurs variables, appelle la fonction OpenLibraries (voir CanDoMJC.h), puis lit et convertit toutes les chaînes de paramètres transmises au programme par le deck CanDo. Le premier paramètre est l'adresse de la structure de données "Window" pour la carte MJPlotPic. La chaîne de caractères est convertie en un entier long non signé qui, à son tour, est converti en un pointeur vers une structure de données Window. Avec cette adresse, le programme C peut dessiner directement sur la carte MJPlotPic. Les autres paramètres sont ceux décrits précédemment et leurs types de données sont convertis de manière appropriée. Une fois les paramètres lus (notez que les deux derniers paramètres ne sont lus que si un tracé d'ensemble de Julia est demandé), l'ensemble de Mandelbrot ou de Julia est tracé. Ensuite, la fonction CloseLibraries (voir CanDoMJC.h) est appelée et le programme se termine.
Le programme CanDoMJC a été compilé comme indiqué dans les listings, sans erreur ni alerte, à l'aide du système de développement SAS/C version 6.50. Les options du compilateur ont été définies de manière à ce que le programme utilise les bibliothèques de virgule flottante IEEE fournies avec AmigaOS. Ce sont les mêmes bibliothèques que celles utilisées par CanDo pour ses calculs en virgule flottante. Ainsi, le code CanDo et le code C sont sur un pied d'égalité lorsqu'il s'agit des calculs en virgule flottante. La différence de vitesse vient du fait que le code C est compilé alors que le code CanDo n'est que semi-compilé. De plus, CanDo passe du temps à convertir entre les types de données alors que le C utilise des variables avec des types de données prédéterminés.
Comparaisons de vitesse
Comme on pouvait s'y attendre, le code C a généré des tracés beaucoup plus rapidement que le code CanDo. Les temps de tracé discutés ci-dessous s'appliquent à mon Amiga 2000 avec une carte accélératrice 68030/68882 28 MHz de GVP.
En général, le code C s'exécute environ 40 à 50 fois plus vite que le code CanDo. Par exemple, l'ensemble de Mandelbrot illustré à la figure 1 (durée maximale de 31) a été généré en 50 secondes avec le code C et en 41 minutes avec le code CanDo. L'ensemble Julia de la figure 6 (durée maximale de 63) a pris 55 secondes en C et 38 minutes en CanDo. Ainsi, pour les programmes CanDo à forte intensité mathématique en virgule flottante, il est conseillé d'écrire un programme de soutien en langage C pour améliorer les performances.

Figure 6 : ensemble de Julia (Dwell maximum=63, ci=-0,75+0,1i)
CanDoMJ a un lien très simple avec son programme C d'arrière-plan. Il suffit de transmettre au programme C une adresse de fenêtre ainsi que quelques autres valeurs numériques. Le programme C fait son travail et se termine. Dans d'autres programmes, une communication bidirectionnelle entre le programme d'interface et le programme C peut être nécessaire. Dans ce cas, les données peuvent être transférées entre les programmes via des fichiers de données sur le périphérique RAM:. Ou, si des communications plus sophistiquées sont nécessaires, des communications ARexx pourraient être ajoutées au programme C. Bien entendu, l'outil de création utilisé pour l'interface doit également gérer les communications ARexx. CanDo le fait.
|












