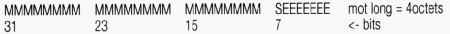Suivez-nous sur X

|
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z,
ALL
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
A propos d'Obligement

|
|
David Brunet

|
|
|
|
Programmation : Assembleur - Les bibliothèques mathématiques (compléments)
(Article écrit par Dominique Genot et extrait d'Amiga News Tech - octobre 1990)
|
|
Nous vous proposons aujourd'hui, un excellent article de complément sur les bibliothèques
mathématiques écrit par le non moins excellent Dominique Genot.
Cet article fait suite à celui de Commodore Revue de mai 1990 (n°23) sur les
bibliothèques mathématiques.
Dans le susdit article étaient abordées les bibliothèques "mathffp" et "mathtrans".
Quelques précisions seront utiles pour les conversions envisagées aujourd'hui :
il s'agit de transformer une chaîne alphanumérique en nombre et lycée de Versailles...
Que veut dire FFP ?
Ces deux bibliothèques permettent de manipuler des nombres entiers ou décimaux qui sont pour
cela stockés sous une forme particulière dite FFP : Fast Floating Point (ou encore flottant en
simple précision). Cela signifie que le nombre n'est pas stocké sous une forme immédiatement
compréhensible. Chaque nombre est codé avec un mot long (4 octets) dont les bits ont la signification suivante :
"M" correspond à la mantisse, codée sur 24 bits. "S" est le signe du nombre. "E"
est la puissance de 2 associée au nombre, codée sur 7 bits (ce mot long est en général placé
dans le registre D0).
J'en vois qui toussent... Prenons un exemple en base 10. Le nombre 41,25 peut aussi s'écrire 0,4125x10
exp 2. Dans cette dernière expression, 0,4125 sera appelée la mantisse du nombre et 10 exp 2
est la puissance de 10 associée. Cette écriture signifie que pour retrouver le nombre, il faut prendre
la mantisse 0,4125 dans laquelle on décale la virgule deux fois vers la droite.
Dans le cas général, la mantisse est un nombre compris entre 1/10 et 1, donc la mantisse est supérieure
ou égale à 0,1 et inférieure à 1 et l'exposant indique le nombre de décalages que la virgule a subi
en base 10. Or, notre génial microprocesseur calcule en base 2, et il écrira donc les nombres sous la
forme : mantisse x 2 exp n.
Dans ce cas, la mantisse est un nombre compris entre 1/2 et 1, donc un nombre supérieur ou égal à 0,5 et
inférieur à 1 et l'exposant indiquera le nombre de décalages que la virgule a subi quand le nombre est
écrit en base 2 (cette écriture est repérée en assembleur par le signe %).
Exemple : le nombre 5 peut s'écrire %101, on aura donc comme mantisse %0,101 dans les bits 8 à 31
(en complétant à droite avec des 0), le bit 7 sera mis à 0, et l'exposant +3 (décaler trois
fois la virgule à droite pour retrouver le nombre) est codé avec les bits 0 à 6.
Remarque : dans tous les cas, il faut coder le signe de l'exposant, c'est-à-dire le sens de
décalage de la virgule. En réalité, l'exposant est codé en notation "excess-64" : ce terme aussi
barbare qu'intraduisible signifie que l'exposant peut varier de -64 (-$40) à +63 (+$3F) et il sera
codé de 0 à 127($7F) (NDLR : l'exposant -$40 est codé par 0 et l'exposant +$3f est codé par 127).
Dans l'exemple du nombre 5, l'exposant 3 sera codé avec $43 (%100 0011) donc % (0,) 10100000 00000000
00000000 01000011 soit $ A0000043
C'est cette valeur que l'on obtient (dans D0) en appelant SPFIt avec 5 dans D0
en mode trace... (NDLR : par mode trace, l'auteur entend le suivi pas à pas du programme
avec un débogueur quelconque (Seka Devpac...), rien à voir avec le mode trace du 68000).
Cette connaissance est-elle vraiment nécessaire ? Elle ne l'est pas pour faire des calculs, car
les bibliothèques ont des routines qui convertissent automatiquement (voir
cet article : les décalages
SPFixet SPFIt). Ces détails sont pourtant utiles pour connaître la précision du
calcul effectué. En effet, le plus grand nombre manipulable est calculé en fixant tous les bits
à 1 (sauf les bits de signes), ce qui donne :
Soit finalement : 9,22337177x10 exp 18, ce qui nous laisse de beaux jours ! Cela prouve qu'il
n'y a guère de limitation en taille, à moins de faire un calcul astronomique (comme le montant
de ses impôts ?).
Ce qui limite davantage, c'est le codage de la mantisse car on ne lui accorde que 24 bits
soit au maximum le nombre 0,16777215 soit huit chiffres significatifs dans le meilleur des cas...
Ceci explique certaines bizarreries où un calcul donne 12,239999... au lieu de 12,24.
Comment remédier à cela ? En accordant davantage de bits à la mantisse, c'est le mode IEEE.
Que veut dire IEEE ?
C'est l'autre façon de coder un nombre flottant et on l'appelle parfois "double précision"
dans un souci de clarté bien compréhensible... Le nombre est alors stocké sur deux
mots longs (8 octets) sous la forme suivante :
...avec les mêmes conventions : "M" désigne la mantisse codée sur 52 bits,
"S" est le signe du nombre IEEE, "E" est la puissance de deux correspondante, codée sur 11 bits.
Cette notation autorise tous les nombres entre -1,8x10 exp 307 et 1,8x10 exp 307 et
surtout elle est beaucoup plus précise car la mantisse peut aller jusqu'à $F FFFF FFFF FFFF !
(ce qui autorise 16 chiffres significatifs).
Attention : des erreurs d'approximation peuvent se produire si le nombre comporte
plus de 16 chiffres...
Bien sûr, d'autres bibliothèques sont à utiliser pour ce mode IEEE. Voici un tableau récapitulatif :
Sur ces quatre bibliothèques, seule la "mathffp" est en ROM, et les trois
autres doivent donc figurer dans le tiroir Libs: de votre disquette système.
Pour simplifier les choses :
- Les décalages valables pour la bibliothèque "mathffp" le sont aussi pour la bibliothèque
"mathieeedoubbas" et idem pour les deux autres. Ce qui est important, c'est de penser
qu'en mode IEEE, les nombres nécessitent deux mots longs pour être manipulés et mis en mémoire
(sinon bonjour le Guru !). Les nombres sont donc associés à des paires de registres :
D0/D1 (opérations courantes) et D2/D3.
- Les conditions d'entrée et de sortie des routines sont les mêmes que pour les deux premières
bibliothèques à condition de raisonner sur des paires de registres en mode IEEE.
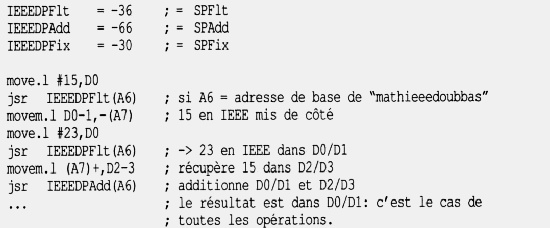
Exemple : pour additionner 15 et 23 en double précision (la bibliothèque "mathieeedoubbas"
est supposée ouverte) :
On peut ajouter jsr IEEEDPFix(A6) pour voir le résultat entier dans D0 en mode trace soit 38 (ou $26).
Dans la pratique, il suffit de nommer les décalages le plus simplement possible, IEEEDPFIt ->
FIt par exemple, et de régler A6 sur une bibliothèque FFP ou IEEE suivant le type de
calcul à effectuer (ou utiliser bien sûr des fichiers "include").
Important : une remarque cependant sur les bibliothèques IEEE : toute tâche qui
les utilise doit les ouvrir elle-même (et non pas récupérer ailleurs un pointeur sur
l'adresse de base) car ces bibliothèques sont reliées à la structure de la tâche qui les a ouvertes.
Changement de mode
On peut désirer convertir un nombre FFP en nombre IEEE ou l'inverse. D'après le ROM Kernal Manual
"Libraries and Devices", il semble qu'il existe un mode hybride appelé "ieee simple précision"
codé sur un registre seulement... Il existe en tout cas deux
décalages de traduction dans les mathtrans...library :
A titre indicatif, voici une routine qui permet de convertir un nombre IEEE en nombre FFP
(les bibliothèques sont supposées ouvertes) :
La conversion inverse 321 (FFP) donne 329 (IEEE) ! Ces routines seraient-elles boguées ?
(NDLR : il semble effectivement que cela soit le cas pour Fieee de mathieeedoubtrans.
Pour preuve, les développeurs du compilateur Lattice C ont réécrit ces routines).
Une dernière chose avant de passer à la pratique : pour les programmeurs en C, le mode
FFP correspond à la déclaration "float" et le mode IEEE correspond à la déclaration "double".
Le C possède bien les fonctions float=afp (chaîne) et fpa (float,chaine) mais ces
fonctions travaillent en mode FFP et sont imprécises si le nombre comporte une dizaine de chiffres.
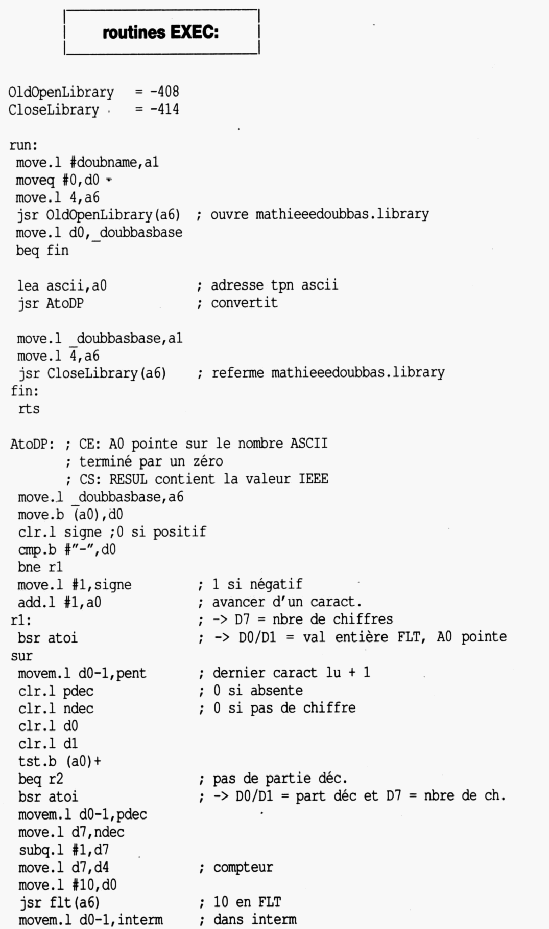
Conversion ASCII -> flottant
Dans ce qui suit, on suppose que le nombre à convertir est stocké sous forme ASCII dans une chaîne terminée par
un octet 0 (voir l'étiquette "ascii" dans le source-exemple). La chaîne est considérée comme formée de quatre parties :
- Le signe "+" ou "-" au début (pas de signe est interprété comme "+").
- La partie entière.
- Un séparateur qui peut être une virgule ou un point.
- La partie décimale.
Pour convertir la chaîne :
- La partie entière est convertie en flottant FFP ou IEEE.
- La partie décimale est convertie en flottant FFP ou IEEE.
- Le nombre de chiffres après la virgule est calculé, appelons-le "n".
- La partie décimale flottante est alors divisée par 10 exp n puis additionnée à la partie entière flottante.
- On tient enfin compte du signe si la chaîne commençait par "-".
Exemple : la chaîne "-123.45" donnerait :
- 123 en flottant.
- 45 en flottant et deux chiffres après la virgule.
- 45 / 10 exp 2 (soit 0,45) additionné à 123 en flottant, donc 123,45.
- On prend l'opposé du résultat avec jsr Neg(a6), donc -123,45.
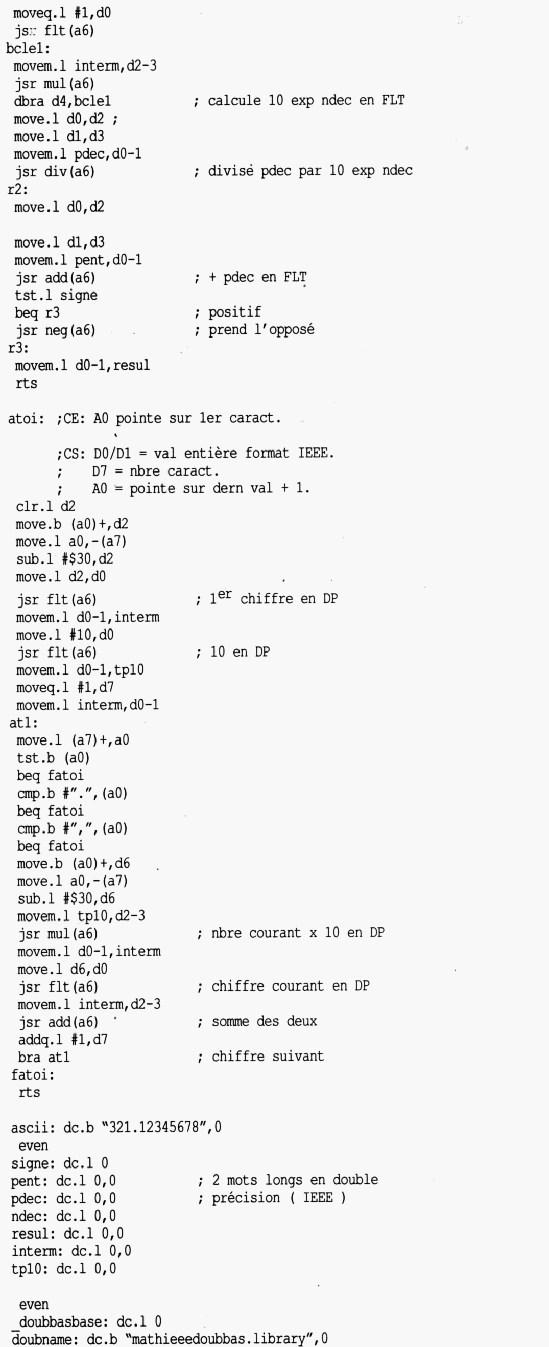
Pour convertir un entier ASCII en flottant :
- Chaque chiffre est lu, on lui enlève $30 (valeur ASCII de 0) pour avoir sa valeur.
- On multiplie le total que l'on avait par 10 et on y ajoute ce dernier chiffre.
Exemple : pour convertir "123", on aura successivement comme total : 0x10+1(lu),
puis 1x10+2(lu) soit 12, puis 12x10+3(lu) soit 123, c'est ce que fait la routine "atoi".
Ce source fonctionne mais il n'est pas possible de vérifier à la fin le résultat à moins de le multiplier
par 100, de prendre la valeur absolue avec jsr Neg(A6) et de le convertir en entier avec jsr Fix(A6).
En mode trace, cela affichera D0=12345 soit $3039.
Je vous laisse découvrir les limites de ce mode en essayant plusieurs chaînes ASCII
de la forme : "-4578,5","458.67849", etc.
Pour la conversion en mode IEEE, les routines sont légèrement compliquées car il faut considérer
des paires de registres, mais le principe est le même :
Conversion FLT -> ASCII
Le principe est très peu différent, les opérations étant effectuées en sens inverse. L'exemple suivant
convertit un nombre IEEE en une chaîne ASCII, il est à modifier (assez peu) pour convertir un nombre FFP
en une chaîne ASCII.
La routine "rectif" qui est appelée est une astuce : comme une erreur de calcul est souvent faite sur
le dernier chiffre de la partie décimale, on ajoute 0,000 000 000 5 au nombre pour que l'erreur
se produise sur un chiffre qui ne compte pas, car on ne garde que les neuf
premiers chiffres... On pourrait passer comme paramètre de la routine DPtoA le nombre de
chiffres à prendre dans la partie décimale, l'instruction move.l #1000000000,d0
de "DPtoA" serait remplacée par une boucle du genre :
La routine "rectif' serait alors ajustée en conséquence...
Applications
Un des avantages de la routine DPtoA est qu'elle permet de vérifier en mode trace
la validité d'un calcul : il suffit de l'appeler pour traduire le nombre calculé
D0/D1 en chaîne ASCII que l'on visualise à l'aide du traceur (fenêtre 3 de Devpac
en mode trace = "monam2").
Elle pourrait aussi permettre de déboguer un programme de calcul vicieux qui méditerait
trop souvent si vous voyez ce que je veux dire... Par exemple, et pour répondre à la question
d'un GL (Gentil Lecteur) du club "Mais-dis-tu-rame-hé", supposons que l'on soit pris
d'un désir irrépressible de calculer le carré de e=2,718,
on remplacerait la partie "run" du programme précédent par celle-ci :
Après lancement, si on regarde (ou si on écrit à l'écran) la chaîne "asc2", on voit
- ô miracle - qu'elle contient la valeur ardemment cherchée, soit 7,....
ce qui suscitera en vous une joie ineffable, ô ami GL.
|