Suivez-nous sur X

|
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z,
ALL
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
A propos d'Obligement

|
|
David Brunet

|
|
|
|
En pratique : Algorithmes et structures de données - Les listes chaînées
(Article écrit par Lucien Turski-Marcon et Bruno Bailluet et extrait d'Amiga News Tech - janvier 1992)
|
|
Cette nouvelle rubrique "Algorithmes et structures de données" aura pour but de vous présenter
chaque mois un exemple d'utilisation des structures de données, à travers quoi ? A travers un algorithme, oui.
Pour notre premier article, nous allons aborder les listes doublement et simplement chaînées.
Et pour commencer, une petite définition : une liste chaînée est une structure de données dynamiques.
Il s'agit d'un noeud composé de deux parties : un morceau information et un autre morceau, appelé lien,
qui permet de chaîner les noeuds entre eux. Le schéma ci-dessous résume parfaitement la structure d'une
liste chaînée.
 Schéma 1
Schéma 1
Statique, dynamique : différences
Afin de bien comprendre ce qui sépare ces deux organisations, effectuons un parallèle entre le
tableau (statique) et la liste (dynamique).
Le tableau
- Taille prédéfinie : il faut connaître à l'avance ses besoins en espace de façon bien précise.
En effet, la taille du tableau doit être initialisée dans le code source du programme.
- Taille figée : cette deuxième restriction découle de la première. En effet, une fois le code
source compilé, l'on ne peut plus modifier (de façon décente) la taille d'un tableau, et ceci
pendant toute la durée d'éxecution du programme.
La liste chaînée
- Taille non prédéfinie : l'on n'est pas obligé de connaître la quantité exacte de données nécessaires
à l'application. Le schéma 1 montre très bien que rien n'empêche d'ajouter un autre noeud à la liste.
- Taille modulable : l'on peut aussi supprimer un élément de la liste. De ce fait, nous voyons que notre
liste peut croître ou décroître à volonté. Ceci est d'autant plus intéressant que toutes ces modifications
peuvent intervenir pendant l'exécution du programme, en fonction des besoins de l'utilisateur. Exemple :
un répertoire téléphonique comporte trois noms. Représentons-les à l'aide de nos deux types de structures
(Cf. schéma 2).
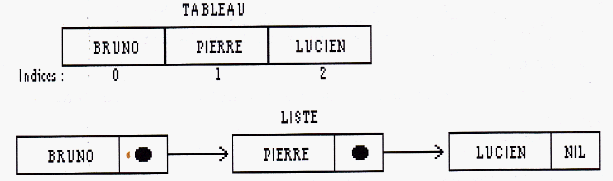 Schéma 2
Schéma 2
Jusque-là, tout est correct. A présent, ajoutons un élément "Franck" (Cf. schéma 3). Nous venons de voir à quel
point il est facile d'ajouter un élément dans la liste. En revanche, le tableau n'accepte pas le nom supplémentaire,
car il n'y a plus de place.
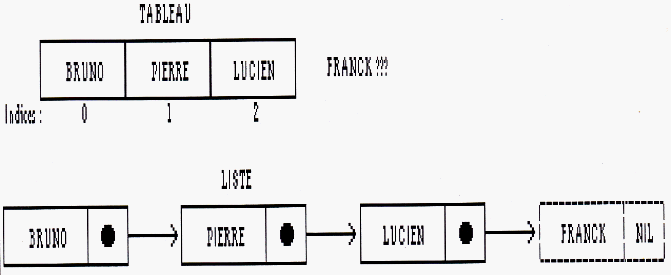 Schéma 3
Schéma 3
Supprimons maintenant deux éléments, "Bruno" et "Lucien" (Cf. schéma 4). Bien que nous ayons supprimé deux prénoms,
le tableau conserve sa taille initiale et les "cases" non utilisées occupent toujours de l'espace mémoire.
Au contraire, la liste chaînée est réduite à son strict minimum. Les emplacements occupés par les noeuds
supprimés ont été restitués au système.
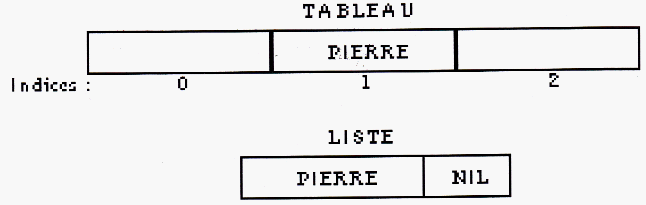 Schéma 4
Schéma 4
Primitives
Maintenant que les listes nous sont familières, nous allons étudier les différentes opérations que nous pouvons
leur faire subir. Les primitives sont en pseudo-code et elles concernent les listes simplement et doublement chaînées.
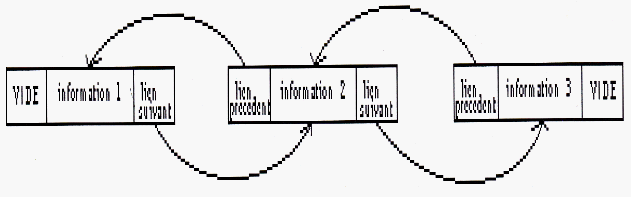 Schéma 5
Schéma 5
La liste double ne diffère de la simple que par la présence d'un lien supplémentaire, qui relie chaque noeud à
son prédécesseur, permettant ainsi de parcourir la liste dans les deux sens.
Insertion
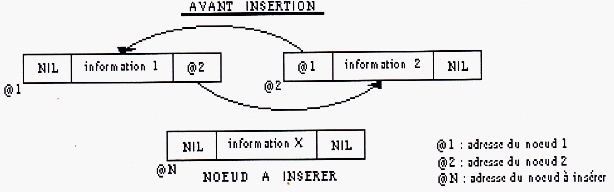 Schéma 6
Schéma 6
(1) noeud2_adr <- noeudl.suivant;
(2) noeud1.suivant <- nouveau noeud;
(3) nouveau noeud.précédent <- noeudl;
(4) nouveau_noeud.suivant <- noeud2_adr;
(5) noeud2_adr.précédent <- nouveau_noeud;
Les étapes (3) et (5) ne concernent pas les listes simplement chaînées.
 Schéma 7
Schéma 7
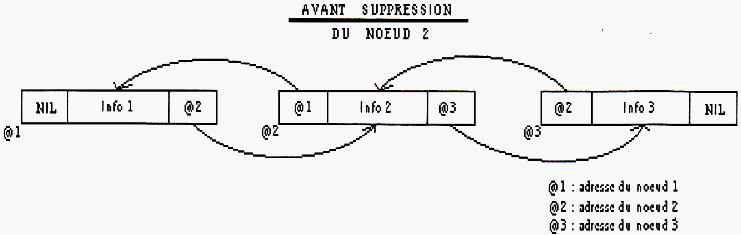 Schéma 8
Schéma 8
Suppression
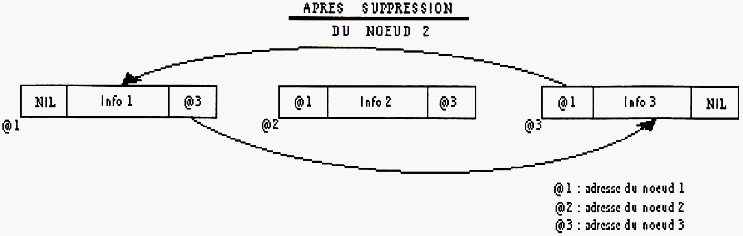 Schéma 9
Schéma 9
(1) noeud1.suivant <- noeud2.suivant;
(2) noeud3_adr <- noeud2.suivant;
(3) noeud3_adr.précédent <- noeud1;
Seule l'étape (1) est nécessaire aux listes simplement chaînées.
Application
Après avoir été très théoriques, passons à des exemples pratiques. Les programmes présentés ci-dessous
permettent d'insérer et de supprimer des noeuds d'une liste. L'insertion se fait en fin de liste,
alors que la suppression se fait par la recherche de l'élément à supprimer. Le source Pascal traite
le problème à travers une liste simplement chaînée, tandis que celui en C utilise une liste doublement
chaînée.
En Pascal
{ compilation : }
{ Pascal src1.pcq src1.asm }
{ A68k src1.asm }
{ Blink src1.o to src1 library pcq.lib }
Program liste_chaînee ;
type { definition des modeles }
noeud = Record { structure de la liste }
num : integer ; { champ info ; ici un numero }
suivant : ^noeud;{ pointeur sur le noeud suivant }
end;
lien = ^noeud ;
var { declaration des variables }
debut : lien ; { pointeur qui memorisera le }
{ debut de notre liste }
choix : integer ;
numero : integer ;
key : char ;
procedure affiche_liste ;
var
element_courant : lien ; { necessaire pour parcourir la }
{ liste sans perdre le debut }
begin
element_courant := debut ;{ se place au debut }
{ afficher le num du noeud courant tant que son pointeur}
{ suivant est different de la fin de liste }
while (element_courant^.suivant <> NIL) do
begin
writeln ('numero : ', element_courant^.num) ;
element_courant := element_courant^.suivant ;
end ;
{ afficher le numero du dernier noeud }
writeln ('numero : ', element_courant^.num) ;
end ;
procedure insere(info : integer) ;
var
element_courant, element_insere : lien ;
begin
element_courant := debut ;
{ recherche de la fin de liste afin d'y ajouter un noeud }
while (element_courant^.suivant <> NIL) do
element_courant := element_courant^.suivant ;
{ allocation de l'espace memoire pour le nouveau noeud }
new (element_insere) ;
element_courant^.suivant := element_insere ;
element_insere^.num := info ;
element_insere^.suivant := NIL ;
affiche_liste ;
end ;
procedure supprime(info2 : integer) ;
var
element_courant, element_supprime : lien ;
begin
element_courant := debut ;
{ detecte le noeud a supprimer et la fin de liste }
{ on va toujours verifier le numero du noeud suivant }
{ de ce fait on empeche la suppression de debut si}
{ l'on saisit 0 comme num }
while (element_courant^.suivant^.num <> info2) and
(element_courant^.suivant <> NIL) do
element_courant := element_courant^.suivant ;
{ test pour savoit si fin de liste ou numero trouve }
if (element_courant^.suivant <> NIL) then
begin
element_supprime := element_courant^.suivant ;
element_courant^.suivant := element_supprime^.suivant ;
dispose (element_supprime) ;
end
else
writeln ('l element n existe pas') ;
affiche_liste ;
end ;
begin
choix := 0 ;
new(debut) ; debut^.suivant := NIL ; debut^.num := 0 ;
repeat
writeln ('1 inserer numero') ;
writeln ('2 supprimer numero') ;
writeln ('9 sortir') ;
write ('votre choix : ') ; readln (choix) ;
case choix of
1 : begin
write ('numero a inserer : ') ; readln (numero) ;
insere(numero) ;
writeln ('pressez enter pour continuer') ;
read (key) ;
end ;
2 : begin
write ('numero a supprimer : ') ;
readln (numero) ;
supprime(numero) ;
writeln ('pressez enter pour continuer') ;
read (key) ;
end ;
end ;
until (choix = 9) ;
dispose (debut) ;
end.
|
En C
/* lc -L liste.c */
#include <exec/types.h>
#include <stdlib.h>
#include <stdio.h>
struct Noeud {
struct Noeud *precedent;
int information;
struct Noeud *suivant;
};
struct Noeud *debut;
VOID Insere (int);
VOID Supprime (int);
VOID AfficheListe (VOID);
VOID main (VOID)
{
int nombre, choix;
debut = (struct Noeud *) malloc (sizeof (struct Noeud));
debut -> precedent = NULL;
debut -> information = -1;
debut -> suivant = NULL;
do
{
printf ("1. Inserer nombre\n");
printf ("2. Supprimer nombre\n");
printf ("3. Sortir\n");
printf ("\n\nVotre choix : ");
scanf ("%d",&choix);
switch (choix)
{
case 1 :
printf ("\n\nNombre a inserer : ");
scanf ("%d",&nombre);
Insere (nombre);
printf ("Pressez une touche pour continuer...\n");
getchar ();
break;
case 2 :
printf ("\n\nNombre a supprimer : ");
scanf ("%d",&nombre);
Supprime (nombre);
printf ("Pressez une touche pour continuer...\n");
getchar ();
break;
}
AfficheListe ();
} while (choix != 3);
}
VOID Insere (int nbre)
{
struct Noeud *courant, *nouveau;
for (courant = debut; courant -> suivant ; courant = courant -> suivant);
nouveau = (struct Noeud *) malloc (sizeof (struct Noeud));
courant -> suivant = nouveau ;
nouveau -> precedent = courant ;
nouveau -> suivant = NULL;
nouveau -> information = nbre;
}
VOID Supprime (int nbre)
{
struct Noeud *courant, *precedent, *suivant;
courant = debut;
while ((courant -> suivant != NULL) &&
(courant -> information != nbre))
courant = courant -> suivant;
if ((courant -> information == nbre) && (courant -> precedent != NULL))
{
precedent = courant -> precedent ;
suivant = courant -> suivant ;
precedent -> suivant = suivant ;
suivant -> precedent = precedent ;
free ((char *) courant);
}
else
printf ("Element non trouve !!!\n");
}
VOID AfficheListe (VOID)
{
struct Noeud *courant;
int i;
for (courant = debut, i = 0; courant -> suivant;
courant = courant -> suivant, i++)
printf ("Noeud %d : %d\n",i,courant -> information);
printf ("Dernier Noeud : %d\n",courant -> information);
}
|
|























